题目内容
9.如果x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$,这就是一元二次方程根与系数的关系(韦达定理).利用韦达定理解决下面问题:已知m与n是方程x2-5x-25=0的两根,则$\frac{n}{m}$+$\frac{m}{n}$=-3.分析 由根与系数的关系可得出m+n=5、m•n=-25,将$\frac{n}{m}$+$\frac{m}{n}$变形为$\frac{(m+n)^{2}-2mn}{mn}$,代入数据即可得出结论.
解答 解:∵m与n是方程x2-5x-25=0的两根,
∴m+n=5,m•n=-25,
∴$\frac{n}{m}$+$\frac{m}{n}$=$\frac{{m}^{2}+{n}^{2}}{mn}$=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{{5}^{2}-2×(-25)}{-25}$=-3.
故答案为:-3.
点评 本题考查了根与系数的关系,根据根与系数的关系找出m+n=5、m•n=-25是解题的关键.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
19. 如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
 如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )
如图所示,∠1=∠2=∠3=∠4,则AD是△ABC的( )| A. | 高 | B. | 角平分线 | C. | 中线 | D. | 以上都不是 |
4.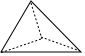 甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
(1)计算此次实验中出现向下面数字为4的频率;
(2)如果甲、乙两同学各抛一枚这样的骰子,请用表格或树状图表示:两枚骰子向下面数字之和的所有等可能性结果,并求出和为3的倍数的概率.
 甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:
甲同学做抛正四面体骰子(如图:均匀的正四面体形状,各面分别标有数字1、2、3、4)实验,共抛了60次,向下面数字出现的次数如表:| 向下面数字 | 1 | 2 | 3 | 4 |
| 出现次数 | 11 | 16 | 18 | 15 |
(2)如果甲、乙两同学各抛一枚这样的骰子,请用表格或树状图表示:两枚骰子向下面数字之和的所有等可能性结果,并求出和为3的倍数的概率.
 如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.
如图,在△ABC中,∠C=100°,BD平分∠ABC交AC于点D,AP平分∠BAC交BD于点P,求∠APD的度数.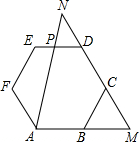 如图所示,正六边形ABCDEF中,P是ED上一点,直线DC与AP、AB延长线分别相交于点N、M.若三角形AMN和正六边形ABCDEF的面积相等,EP:PD=1:2.
如图所示,正六边形ABCDEF中,P是ED上一点,直线DC与AP、AB延长线分别相交于点N、M.若三角形AMN和正六边形ABCDEF的面积相等,EP:PD=1:2.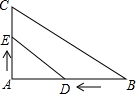 在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?
在Rt△ABC中,A=90°,AB=8,AC=6,若动点D从点B出发,沿线段BA运动到点A为止,速度是每秒2个单位;动点E从点A出发,沿线段AC运动,每秒1个单位,两点同时出发,运动多长时间,△ADE与△ABC相似?