题目内容
已知a,b,c满足|2a-4|+|b+2|+
+a2+c2=2+2ac,且b≠0,则函数y=ax2-bx+c的最小值是 .
| (a-3)b2 |
考点:二次函数的最值,非负数的性质:偶次方,二次根式有意义的条件,配方法的应用
专题:计算题
分析:根据非负数的性质求出a、b、c的值,得到函数解析式,利用解析式即可求出函数y=ax2-bx+c的最小值.
解答:解:
∵|2a-4|+|b+2|+
+a2+c2=2+2ac,
移项得|2a-4|+|b+2|+
+a2+c2-2ac=2,
整理得|2a-4|+|b+2|+
+(a-c)2=2.
当b不等于0
则 b2>0,
则(a-3)≥0,
∴a≥3,
∵a≥3,
∴|2a-4|≥2,
∵各部分都大于0且等号右边为2,
∴|2a-4|=2,
a=3,
再整理得|b+2|+(a-c)2=0,
b=-2,
a=c=3,
∴函数y=ax2-bx+c的解析式为y=3x2+2x+3=3(x+
)2+
;
∴函数最小值为
.
故答案为
.
∵|2a-4|+|b+2|+
| (a-3)b2 |
移项得|2a-4|+|b+2|+
| (a-3)b2 |
整理得|2a-4|+|b+2|+
| (a-3)b2 |
当b不等于0
则 b2>0,
则(a-3)≥0,
∴a≥3,
∵a≥3,
∴|2a-4|≥2,
∵各部分都大于0且等号右边为2,
∴|2a-4|=2,
a=3,
再整理得|b+2|+(a-c)2=0,
b=-2,
a=c=3,
∴函数y=ax2-bx+c的解析式为y=3x2+2x+3=3(x+
| 1 |
| 3 |
| 8 |
| 3 |
∴函数最小值为
| 8 |
| 3 |
故答案为
| 8 |
| 3 |
点评:本题考查了二次函数的最小值,根据非负数的性质求出函数解析式是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
满足
<x<
的整数x的个数是 ( )
| 1 | ||||
|
| 2 | ||||
|
| A、4 | B、5 | C、6 | D、7 |
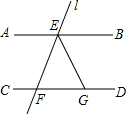 如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )
如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )| A、115° | B、125° |
| C、130° | D、100° |
 如图是由三个棱长为1的正方体组成的几何体,则从前往后看得到的投影是( )
如图是由三个棱长为1的正方体组成的几何体,则从前往后看得到的投影是( )A、 |
B、 |
C、 |
D、 |
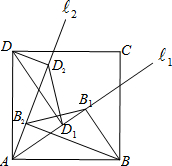 如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由.
如图,在正方形ABCD中,从点A引两条射线?1,?2,分别过点B、D作?1,?2的垂线,垂足为B1,B2,D1,D2,连接B1B2、D1D2.试探求B1B2与D1D2之间数量的关系,并说明理由. 如图,⊙O 是△ABC 的外接圆,BC=a,CA=b,且∠A-∠B=90°.则⊙O的半径为
如图,⊙O 是△ABC 的外接圆,BC=a,CA=b,且∠A-∠B=90°.则⊙O的半径为