题目内容
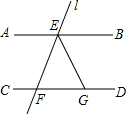 如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )
如图,AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=50°,则∠EGD的度数是( )| A、115° | B、125° |
| C、130° | D、100° |
考点:平行线的性质
专题:
分析:由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,即可得∠GEF的度数,然后利用三角形外角的性质,即可求得∠EGD的度数.
解答:解:∵AB∥CD,
∴∠BEF+∠EFG=180°,
∵∠EFG=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠GEF=
∠BEF=65°,
∴∠EGD=∠GEF+∠EFG=65°+50°=115°.
故选A.
∴∠BEF+∠EFG=180°,
∵∠EFG=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠GEF=
| 1 |
| 2 |
∴∠EGD=∠GEF+∠EFG=65°+50°=115°.
故选A.
点评:此题考查了平行线的性质、角平分线的定义以及三角形外角的性质.此题难度不大,解题的关键是掌握两直线平行,同旁内角互补定理的应用,掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设m,n是方程x2-x-2012=0的两个实数根,则m2+n的值为( )
| A、1006 | B、2011 |
| C、2012 | D、2013 |
 如图,已知矩形OABC的面积为81,它的对角线OB与双曲线
如图,已知矩形OABC的面积为81,它的对角线OB与双曲线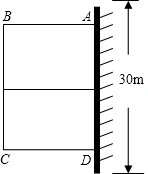 某小区为了改善居住环境,准备修建一个矩形花园ABCD,为了节约材料并种植不同类花,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块,已知所用栅栏的总长为60米,墙长为30米(如图),设花园垂直于墙的一边的长为x米.
某小区为了改善居住环境,准备修建一个矩形花园ABCD,为了节约材料并种植不同类花,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块,已知所用栅栏的总长为60米,墙长为30米(如图),设花园垂直于墙的一边的长为x米.