题目内容

已知⊙O1与⊙O2的半径分别为1和2，且它们的两条公切线互相垂直，则圆心距O1O2的长为
 
．
考点：圆与圆的位置关系
专题：
分析：圆D与圆A，B，C的公切线互相垂直，圆D的半径为2，圆A，B，C的半径为1，由勾股定理可分别求得CD，BD，AD的值．
解答：解：如图，圆D与圆A，B，C的公切线互相垂直，圆D的半径为2，圆A，B，C的半径为1，
由勾股定理易得CD=
CG2+DG2
=
2
，
BD=
BS2+HD2
=
10
，
AD=
AH2+DH2
=3
2
．
故答案为：3
2
或
2
或
10
．
点评：本题考查了圆与圆的位置关系，本题利用了切线的性质，正方形和矩形的性质，勾股定理求解．
练习册系列答案
相关题目
尽管受到国际金融危机的影响，但某市经济依然保持了平稳增长．据统计，截止到今年4月底，该市金融机构存款余额约为1193亿元，用科学记数法应记为
 
元．
已知a，b，c满足|2a-4|+|b+2|+
(a-3)b2
+a2+c2=2+2ac，且b≠0，则函数y=ax2-bx+c的最小值是
 
．
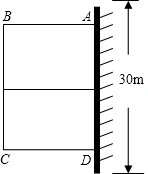某小区为了改善居住环境，准备修建一个矩形花园ABCD，为了节约材料并种植不同类花，决定花园一边靠墙，三边用栅栏围住，中间用一段垂直于墙的栅栏隔成两块，已知所用栅栏的总长为60米，墙长为30米（如图），设花园垂直于墙的一边的长为x米．
（1）若平行于墙的一边长为y米，直接写出y与x的函数关系式及自变量x的取值范围；
（2）当x为何值时，这个矩形花园的面积最大？最大值是多少？（栅栏占地面积忽略不计）；
（3）当这个花园的面积不小于288平方米时，试结合函数图象，直接写出x的取值范围．
设m，n是方程x2-x-2012=0的两个实数根，则m2+n的值为（　　）
A、1006B、2011
C、2012D、2013
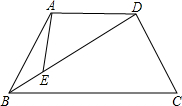如图，在梯形ABCD中，AD∥BC，AB=CD=
10
，BC=5，点E在BD上，且∠BAE=∠DBC．设BD=x，AD=y，求y关于x的函数解析式，并写出函数的定义域．
掷两颗骰子得到两个数，注意大数减去小数的差数，回答下列问题并说明理由．
（1）是否有一个差数比其他差数更容易出现？
（2）现有类似骰子的两个正方体六个面上的数字分别为2、3、4、5、6、7，是否有一个差数更容易出现？数字分别为3、4、5、6、7、8呢？并推广之；
（3）若六个面上数字分别为2、4、6、8、10、12，是否有一个差数更容易出现？数字分别是3、6、9、12、15、18呢？并推广之．
有五张背面相同，正面分别写有数据：
1
3
，
2
，
3
，π，-2的纸牌．充分洗匀后，从中随机抽取一张，抽到无理数的概率为（　　）
A、20%B、40%
C、60%D、80%
（1）“x与2的差不大于-1”所对应的不等式是
 
．
（2）如图，直线a∥b，∠2=42°，则∠1=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网