题目内容
7.在△ABC中,AB=AC,点O为平面上一点且OB=OC,若点A到BC的距离为6cm,点O到BC的距离为4cm,则点A到点O的距离为2cm或10cm.分析 先利用AB=AC,OB=OC可判断点A、O都在BC的垂直平分线上,然后分类讨论:当点O在△ABC的内部时,易得AO=2cm;当点O在△ABC的外部时,易得AO=10cm.
解答 解:∵OB=OC,
∴点O在BC的垂直平分线上,
而AB=AC,
∴点A在BC的垂直平分线上,
当点O在△ABC的内部时,AO=6cm-4cm=2cm;
当点O在△ABC的外部时,AO=6cm+4cm=10cm.
故答案为2cm或10.
点评 本题考查了等腰三角形的性质:等腰三角形的两腰相等,等腰三角形的两个底角相等,等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.

练习册系列答案
相关题目
12.已知关于x的一元二次方程ax2+bx+c=3的一根为x=2,且二次函数y=ax2+bx+c的对称轴是直线x=2,则抛物线的顶点坐标是( )
| A. | (2,3) | B. | (2,1) | C. | (2,-3) | D. | (3,2) |
16.下列说法不正确的是( )
| A. | 对顶角相等 | B. | 矩形的对角线互相平分且相等 | ||
| C. | 菱形的四条边都相等 | D. | 三角形两边的和小于第三边 |
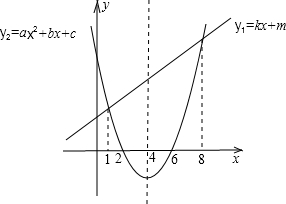 一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图.
一次函数y1=kx+m和二次函数y2=ax2+bx+c的图象如图.