题目内容
18.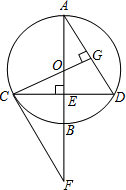 如图,⊙O的直径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
如图,⊙O的直径AB垂直弦CD于E,过点C的切线CF交AB延长线于F,连接CO并延长交AD于G,且CG⊥AD.求证:△CEF≌△DEA.
分析 由CF是⊙O的切线,易得CG⊥CF,证得CF∥AD,得出∠ECF=∠EDA,∠F=∠A,根据垂径定理得出CE=DE,然后根据AAS即可证得△CEF≌△DEA.
解答 证明:∵CF是⊙O的切线
∴∠OCF=90°,
∴CG⊥CF,
又∵CG⊥AD,
∴CF∥AD,
∴∠ECF=∠EDA,∠F=∠A,
∵直径AB垂直弦CD,
∴CE=DE,
在△CEF和△DEA中,
$\left\{\begin{array}{l}{∠ECF=∠EDA}\\{∠F=∠A}\\{CE=DE}\end{array}\right.$,
∴△CEF≌△DEA(ASA).
点评 此题考查了切线的性质、平行线的判定和性质、垂径定理以及全等三角形的判定.熟练掌握性质定理是解此题的关键.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
8.在△ABC中,AB=8,AC=15,BC=17,则该三角形为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 等腰直角三角形 |
9.已知抛物线y=-x2+2x-3,下列判断正确的是( )
| A. | 开口方向向上,y有最小值是-2 | B. | 抛物线与x轴有两个交点 | ||
| C. | 顶点坐标是(-1,-2) | D. | 当x<1时,y随x增大而增大 |
13. 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
 如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )
如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,则所得任一多边形内角和度数不可能是( )| A. | 720° | B. | 540° | C. | 360° | D. | 180° |
3.云南省鲁甸县2014年8月3日发生6.5级地震,造成重大人员伤亡和经济损失.灾情牵动亿万同胞的心,在灾区人民最需要援助的时刻,全国同胞充分发扬“一方有难、八方支援”的中华民族优良传统,及时向灾区同胞伸出援助之手.截至9月19日17时,云南省级共接收昭通鲁甸“8.3”地震捐款80100万元.科学记数法表示为( )元.
| A. | 8.01×107 | B. | 80.1×107 | C. | 8.01×108 | D. | 0.801×109 |
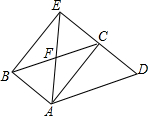 如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长.
如图,在平行四边形ABCD中,AB=$\sqrt{3}$,AC=3,过点B作BE平行AC交DC的延长线于点E,连结AE,AE交BC于点F,若AB⊥AC,求△ADE的周长. 请你根据王老师所给的内容,完成下列各小题.
请你根据王老师所给的内容,完成下列各小题.