题目内容
8．在△ABC中，AB=8，AC=15，BC=17，则该三角形为（ ）| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 等腰直角三角形 |
分析 根据已知可得三边符合勾股定理的逆定理判断即可．
解答 解：∵△ABC中，AB=8，BC=17，AC=17，
∵152+82=172，即AC2+AB2=BC2，
∴三角形是直角三角形，
故选B
点评 本题考查了勾股定理的逆定理：已知三角形ABC的三边满足a2+b2=c2，则三角形ABC是直角三角形．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
如图，△ABC中，AB=BC，∠ABC=120°，E是线段AC上一点，AE=3EC，连接BE并延长至D，连接CD，若∠BCD=120°，AB=6，则线段CD长为3．
16．
已知二次函数y=x2-4x．
（1）在给出的直角坐标系内用描点法画出该二次函数的图象；
（2）根据所画的函数图象写出当x在什么范围内时，y≤0？
（3）根据所画的函数图象写出方程：x2-4x=5的解．
已知二次函数y=x2-4x．（1）在给出的直角坐标系内用描点法画出该二次函数的图象；
（2）根据所画的函数图象写出当x在什么范围内时，y≤0？
（3）根据所画的函数图象写出方程：x2-4x=5的解．
3．
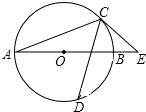如图，AB是⊙O的直径，C，D是⊙O上两点，连接AD，CD，AD=CD，过点C作⊙O的切线交AB的延长线于点E，若∠E=50°，则∠DAC等于（ ）
如图，AB是⊙O的直径，C，D是⊙O上两点，连接AD，CD，AD=CD，过点C作⊙O的切线交AB的延长线于点E，若∠E=50°，则∠DAC等于（ ）| A． | 40° | B． | 50° | C． | 55° | D． | 60° |
如图，AB=4，BC=3，AD=13，DC=12，∠B=90°，求四边形ABCD的面积．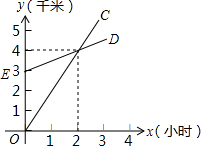
如图，已知A地在B地正南方3千米处，甲乙两人同时分别从A、B两地向正北方向匀速直行，他们的距离s（千米）与所用的时间t（小时）之间的函数关系分别如图中的射线OC和ED，当他们行走4小时后，他们之间的距离为3千米．
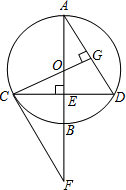如图，⊙O的直径AB垂直弦CD于E，过点C的切线CF交AB延长线于F，连接CO并延长交AD于G，且CG⊥AD．求证：△CEF≌△DEA．