题目内容
8. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=4cm,则⊙O的半径为2$\sqrt{2}$cm.
如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=4cm,则⊙O的半径为2$\sqrt{2}$cm.
分析 连接OC,如图所示,由直径AB垂直于CD,利用垂径定理得到E为CD的中点,即CE=DE,由OA=OC,利用等边对等角得到一对角相等,确定出三角形COE为等腰直角三角形,求出OC的长,即为圆的半径.
解答  解:连接OC,如图所示:
解:连接OC,如图所示:
∵AB是⊙O的直径,弦CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=2cm,
∵OA=OC,
∴∠A=∠OCA=22.5°,
∵∠COE为△AOC的外角,
∴∠COE=45°,
∴△COE为等腰直角三角形,
∴OC=$\sqrt{2}$CE=2$\sqrt{2}$cm,
故答案为:2$\sqrt{2}$.
点评 此题考查了垂径定理,等腰直角三角形的性质,以及圆周角定理,熟练掌握垂径定理是解本题的关键.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
18.关于x的方程x2-4=0的根是( )
| A. | 2 | B. | -2 | C. | 2,-2 | D. | 2,$\frac{1}{2}$ |
3.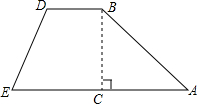 如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
 如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )
如图是拦水坝的横断面,斜坡AB的水平宽度为12m,斜面坡度为1:2,则斜坡AB的长为( )| A. | 4$\sqrt{3}$m | B. | 6$\sqrt{5}$m | C. | 12$\sqrt{5}$m | D. | 24m |

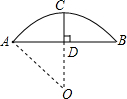 某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?
某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,则中间柱CD的高度为( )米?