题目内容
1．某部队第一天行军5h，第二天行军6h，两天共行军120km，且第二天比第一天多走2km，设第一天和第二天行军的速度分别为xkm/h和ykm/h，则符合题意的二元一次方程是（ ）| A． | 5x+6y=118 | B． | 5x=6y+2 | C． | 5x=6y-2 | D． | 5（x+2）=6y |
分析 根据某部队第一天行军5h，第二天行军6h，两天共行军120km，且第二天比第一天多走2km，设第一天和第二天行军的速度分别为xkm/h和ykm/h，可以列出相应的方程，从而本题得以解决．
解答 解：设第一天和第二天行军的速度分别为xkm/h和ykm/h，
由题意可得，$\left\{\begin{array}{l}{5x+6y=120}\\{6y-5x=2}\end{array}\right.$，
由方程组中6y-5x=2可得，5x=6y-2，
故选项A错误，选项B错误，选项C正确，选项D错误．
故选C．
点评 本题考查由实际问题抽象出二元一次方程，解题的关键是明确题意可以列出相应的方程组，并且可以对方程组中的每个方程进行变形．
练习册系列答案
相关题目
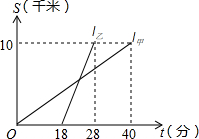甲、乙两人以相同路线前往距离单位10千米的培训中心参加学习，图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（千米）随时间t（分钟）变化的函数图象．以下说法：①从单位到培训中心，乙比甲少用了30分钟；②甲的平均速度为15千米/小时；③乙走了8千米后遇到甲；④乙出发6分钟后追上甲．其中正确的有（ ）
9．
如图，△ABC和△DEF中，AC=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）
如图，△ABC和△DEF中，AC=DE，∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）| A． | AC∥DF | B． | ∠A=∠D | C． | AB=DE | D． | ∠ACB=∠F |
10．
如图，△ABC内接于⊙O，CD是⊙O的直径，∠A=35°，则∠BCD的度数是（ ）
如图，△ABC内接于⊙O，CD是⊙O的直径，∠A=35°，则∠BCD的度数是（ ）| A． | 55° | B． | 65° | C． | 70° | D． | 75° |