题目内容
4.已知关于x的方程为:$\frac{1}{|x-2|}$=$\frac{1}{|x-52a|}$.(1)解这个方程;
(2)若a是一个奇质数的平方,证明这个方程的解是合数.
分析 (1)直接利用完全平方的性质结合平方差公式解方程求出即可;
(2)利用当p=3时,得出26a+1是合数,再利用当p>3时,得出26a+1一定是3的倍数,进而得出也是合数的结论.
解答 解:(1)∵$\frac{1}{|x-2|}$=$\frac{1}{|x-52a|}$,
∴|x-2|=|x-52a|,
∴(x-2)2=(x-52a)2,
整理得:(104a-4)x=2704a2-4,
故(26a-1)x=676a2-1,
解得:x=26a+1;
(2)当p=3时,
26a+1=235 显然是合数,
当p>3时,p2-1=(p+1)(p-1),
因为p是大于3的质数,p一定不是3的倍数,并且p是奇数,
p+1,p-1是两个连续的偶数,必定是8的倍数,
p不是3的倍数,p+1,p-1必定有一个是3的倍数,
所以p2-1是24的倍数,
26a+1=26×(24n+1)+1
=26×24n+27(n是一个整数)
=3(8×26n+9),
故26a+1一定是3的倍数.
故综上所述:这个方程的解是合数.
点评 此题主要考查了解方程以及质数与合数,根据合数的性质得出当p>3时26a+1一定是3的倍数是解题关键.

练习册系列答案
相关题目
9.D、E分别是△ABC的边AB、AC上的点,下列各条件中,不能确定DE∥BC的是( )
| A. | AD=$\frac{1}{3}$AB,AE=$\frac{1}{3}$AC | B. | $\frac{AE}{AC}$=$\frac{3}{5}$,$\frac{DE}{BC}$=$\frac{3}{5}$ | ||
| C. | $\frac{BD}{AD}$=$\frac{3}{2}$,$\frac{AE}{EC}$=$\frac{2}{3}$ | D. | AD=2,DB=3,AE=3,EC=4$\frac{1}{2}$ |
10.已知关于x的方程x2+(6n-m)x+n2+4n+4=0的两个实数根互为相反数,那么m,n的值依次是( )
| A. | 12,2 | B. | 6,1 | C. | -12,-2 | D. | 1,$\frac{1}{6}$ |
14.下列图形和字母,是轴对称图形的是( )
①H ②E ③S ④ ⑤
⑤ ⑥
⑥
①H ②E ③S ④
 ⑤
⑤ ⑥
⑥
| A. | ①②③④⑤ | B. | ①②③ | C. | ①②⑤ | D. | ①②⑤⑥ |
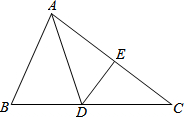 如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.
如图,在△ABC中,DE⊥AC,垂足为E,∠EAD=∠ECD,AE=3cm,△ABD的周长为13cm,试找出图中相等的线段和相等的角并求出△ABC的周长.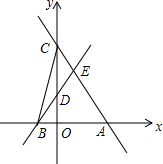 直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
直线y=-$\frac{4}{3}$x+4与x轴交于点A,与y轴交于点C,过点B(-1,0)的直线交线段OC于点D,交线段AC于点E,连接BC,△CDB的面积为1.
 以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状.
以△ABC的边BC为一边向三角形外侧作正方形BDEC,连结AD、AE分别交BC于点F、G,过点F、G分别作BC的垂线交AB、AC于点H、K,试判断四边形HFGK的形状.