题目内容
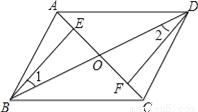
如图，四边形ABCD中，对角线AC，BD相交于点O，点E，F分别在OA，OC上
（1）给出以下条件；①OB=OD，②∠1=∠2，③OE=OF，请你从中选取两个条件证明△BEO≌△DFO；
（2）在（1）条件中你所选条件的前提下，添加AE=CF，求证：四边形ABCD是平行四边形．
（1）见解析；（2）见解析.
【解析】试题分析：（1）选取①②，利用ASA判定△BEO≌△DFO；也可选取②③，利用AAS判定△BEO≌△DFO；还可选取①③，利用SAS判定△BEO≌△DFO；
（2）根据△BEO≌△DFO可得EO＝FO，BO＝DO，再根据等式的性质可得AO＝CO，根据两条对角线互相平分的四边形是平行四边形可得结论．
试题解析：
证明：（1）选取①②，
...
阅读快车系列答案为进一步建设秀美、宜居的生态环境，某村欲购买甲、乙、丙三种树美化村庄，已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，现计划用210000元资金，购买这三种树共1000棵．
（1）求乙、丙两种树每棵各多少元？
（2）若购买甲种树的棵树是乙种树的2倍，恰好用完计划资金，求这三种树各能购买多少棵？
（3）若又增加了10120元的购树款，在购买总棵树不变的前提下，求丙种树最多可以购买多少棵？
（1）200元，200元，（2）能购买甲种树600棵，乙种树300棵，丙种树100棵；（3）丙种树最多可以购买201棵．
【解析】
试题分析：（1）利用已知甲、乙丙三种树的价格之比为2：2：3，甲种树每棵200元，即可求出乙、丙两种树每棵钱数；
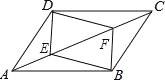
（2）假设购买乙种树x棵，则购买甲种树2x棵，丙种树（1000-3x）棵，利用（1）中所求树木价格以及现计划用210000元资金购买这三... 如图，在?ABCD中，点E，F在对角线AC上，且AE=CF．求证：
（1）DE=BF；
（2）四边形DEBF是平行四边形．
详见解析.
【解析】
试题分析：（1）根据全等三角形的判定方法，判断出△ADE≌△CBF，即可推得DE=BF．（2）首先判断出DE∥BF；然后根据一组对边平行且相等的四边形是平行四边形，推得四边形DEBF是平行四边形即可．
试题解析：（1）∵四边形ABCD是平行四边形，
∴AD∥CB，AD=CB，
∴∠DAE=∠BCF，
在△ADE和△CBF中，
∴△AD... 如图，?ABCD的对角线AC，BD相交于点O，已知AD＝8，BD＝12，AC＝6，则△OBC的周长为( )
A. 13 B. 17 C. 20 D. 26
B
【解析】试题分析：由平行四边形的性质得出OA=OC=3，OB=OD=6，BC=AD=8，即可求出△OBC的周长．
【解析】
∵四边形ABCD是平行四边形，
∴OA=OC=3，OB=OD=6，BC=AD=8，
∴△OBC的周长=OB+OC+AD=3+6+8=17．
故选：B． 在下列条件中，能够判定一个四边形是平行四边形的是（ ）
A. 一组对边平行，另一组对边相等
B. 一组对边相等，一组对角相等
C. 一组对边平行，一条对角线平分另一条对角线
D. 一组对边相等，一条对角线平分另一条对角线
C
【解析】A、错误．这个四边形有可能是等腰梯形．
B、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
C、正确．可以利用三角形全等证明平行的一组对边相等．故是平行四边形．
D、错误．不满足三角形全等的条件，无法证明相等的一组对边平行．
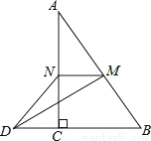
故选C． 如图，在△ABC中，∠ACB=90°，M、N分别是AB、AC的中点，延长BC至点D，使CD=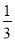
BD，连接DM、DN、MN．若AB=6，则DN=___．
3．
【解析】试题分析：连接CM，根据三角形中位线定理得到NM=CB，MN∥BC，又CD=BD，可得MN=CD，又由MN∥BC，可得四边形DCMN是平行四边形，所以DN=CM，根据直角三角形的性质得到CM=AB=3，即可得DN=3． 如图，?ABCD的对角线AC，BD相交于点O，且AC＋BD＝16，CD＝6，则△ABO的周长是( )
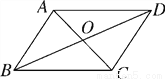
A. 10 B. 14 C. 20 D. 22
B
【解析】试题分析：∵四边形ABCD是平行四边形，∴AO=CO，BO=DO，DC=AB=6，∵AC+BD=16，∴AO+BO=8，∴△ABO的周长是：14．故选B． 已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．
（1）求证：△ABF≌△CDE；
（2）如图，若∠1=65°，求∠B的大小．
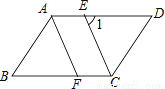
（1）证明见解析；（2）50°．
【解析】试题分析：（1）由平行四边形的性质得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证出∠AFB=∠1，由AAS证明△ABF≌△CDE即可；（2）由（1）得∠1=∠DCE=65°，由平行四边形的性质和三角形内角和定理即可得出结果．
试题解析：（1）∵四边形ABCD是平行四边形， ∴AB=CD，AD∥BC，∠B=∠D， ∴∠1=∠DCE... 抛物线y=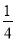
x2+bx+c与x轴交于A(5,0)、B(-1,0)两点，过点A作直线AC⊥x轴，交直线y=2x于点C.
（1）求该抛物线的解析式；
（2）求点A关于直线y=2x的对称点A′的坐标，判定点A′是否在抛物线上，并说明理由；
（3）点P是抛物线上一动点，过点P作y轴的平行线，交线段CA′于点M，是否存在这样的点P，使四边形PACM是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.
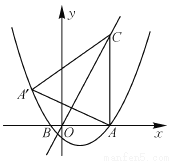
（1）．（2）点A/的坐标为（﹣3,4）．点A/在该抛物线上．（3）点P运动到时，四边形PACM是平行四边形．
【解析】试题分析：（1）将点A、B的坐标代入抛物线的解析式，得到关于b、c的二元一次方程组，从而可解得b、c的值；
（2）过点B′作B′E⊥x轴于E，BB′与OC交于点F．由平行于y轴的直线上各点横坐标相同可知点C的横坐标为2，将x=2代入直线y=﹣2x的解析式可求得点C的坐...