��Ŀ����
6�� ��ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=12cm��BC=18cm����P�ӵ�A������2cm/s���ٶ���A��D��C�˶�����P�ӵ�A������ͬʱ��Q�ӵ�C��������1cm/s���ٶ����B�˶�������P�����Cʱ����QҲֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮
��ͼ�����ı���ABCD�У�AD��BC����B=90�㣬AB=8cm��AD=12cm��BC=18cm����P�ӵ�A������2cm/s���ٶ���A��D��C�˶�����P�ӵ�A������ͬʱ��Q�ӵ�C��������1cm/s���ٶ����B�˶�������P�����Cʱ����QҲֹͣ�˶������P��Q�˶���ʱ��Ϊt�룮��1�����˶���ʼ����tȡ��ֵʱ��PQ��CD��
��2�����˶���ʼ����tȡ��ֵʱ����PQCΪֱ�������Σ�
���� ��1����֪AD��BC������PD=CQ�����ж���PQDCΪ������ı�����ƽ���ı��Σ�
��2����P������Ϊֱ�ǣ���Q��Ҳ������ֱ�ǣ�������⼴�ɣ�
��� �⣺��1����PQ��CDʱ���ı���PDCB��ƽ���ı��Σ�
��ʱPD=QC��
��12-2t=t��
��t=4��
�൱t=4ʱ���ı���PQDC��ƽ���ı��Σ�
��2����D�㣬DF��BC��F��
��DF=AB=8��
FC=BC-AD=18-12=6��CD=10��
�ٵ�PQ��BC��
��BQ+CQ=18������2t+t=18��
��t=6��
�ڵ�QP��PC����ʱPһ����DC�ϣ�
CP1=10+12-2t=22-2t��CQ2=t��
��֪����CDF�ס�CQ2P1��
��$\frac{22-2t}{6}=\frac{t}{10}$��
��ã�t=$\frac{110}{13}$��
�����Σ���PC��BCʱ�����DCB��90�㣬�������β����ڣ�
�൱t=6��$\frac{110}{13}$ʱ����PQC��ֱ�������Σ�
���� ������Ҫ������һ��Ա�ƽ������ȵ��ı�����ƽ���ı����Լ�Բ��Բ��λ�ù�ϵ��֪ʶ��ע���������ۺͳ���֪ʶ��Ӧ�ã�

��ϰ��ϵ�д�
�����Ŀ
16��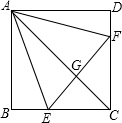 ��ͼ����֪��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G���������н��ۣ�
��ͼ����֪��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G���������н��ۣ�
��BE=DF���ڡ�DAF=15�㣻��AC��ֱƽ��EF����BE+DF=EF��
���н�����ȷ�Ĺ��У�������
 ��ͼ����֪��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G���������н��ۣ�
��ͼ����֪��������ABCD�У���E��F�ֱ���BC��CD�ϣ���AEF�ǵȱ������Σ�����AC��EF��G���������н��ۣ���BE=DF���ڡ�DAF=15�㣻��AC��ֱƽ��EF����BE+DF=EF��
���н�����ȷ�Ĺ��У�������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
17�����и�ʽ�У��������θ�ʽ��Ϊ��������
| A�� | $\sqrt{8a}$ | B�� | $\sqrt{{a}^{2}+{b}^{2}}$ | C�� | $\sqrt{0.1x}$ | D�� | $\sqrt{{a}^{5}}$ |
11���й���������ij�յ���Ⱦָ�����±��������������е���λ���ǣ�������
| ���� | ���� | �Ϸ� | �Ͼ� | ������ | �ɶ� | ֣�� |
| ��Ⱦָ�� | 342 | 163 | 165 | 45 | 227 | 163 |
| A�� | 105 | B�� | 163 | C�� | 164 | D�� | 165 |
18������˵����ȷ���ǣ�������
| A�� | ͬλ����� | B�� | �Զ������ | ||
| C�� | ��ȵĽ�һ���ǶԶ��� | D�� | �ǵĴ�С��ߵij����й� |

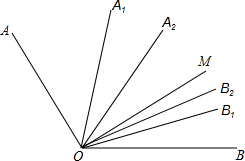 ��ͼ��AOB=���㣬OA1��OB1�ֱ��ǡ�AOM�͡�MOB��ƽ���ߣ�OA2��OB2�ֱ��ǡ�A1OM�͡�MOB1��ƽ���ߣ�OA3��OB3�ֱ��ǡ�A2OM�͡�MOB2��ƽ���ߡ�OAn��OBn�ֱ��ǡ�An-1OM�͡�MOBn-1��ƽ���ߣ����AnOBn=$\frac{1}{{2}^{n}}$���㣮
��ͼ��AOB=���㣬OA1��OB1�ֱ��ǡ�AOM�͡�MOB��ƽ���ߣ�OA2��OB2�ֱ��ǡ�A1OM�͡�MOB1��ƽ���ߣ�OA3��OB3�ֱ��ǡ�A2OM�͡�MOB2��ƽ���ߡ�OAn��OBn�ֱ��ǡ�An-1OM�͡�MOBn-1��ƽ���ߣ����AnOBn=$\frac{1}{{2}^{n}}$���㣮 ��ͼ����֪AB��CD����A=60�㣬��C=20�㣬���E=40�㣮
��ͼ����֪AB��CD����A=60�㣬��C=20�㣬���E=40�㣮