题目内容
1.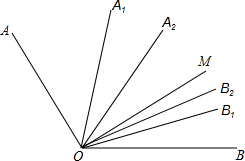 如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°.
如图∠AOB=α°,OA1、OB1分别是∠AOM和∠MOB的平分线,OA2、OB2分别是∠A1OM和∠MOB1的平分线,OA3、OB3分别是∠A2OM和∠MOB2的平分线…OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,则∠AnOBn=$\frac{1}{{2}^{n}}$α°.
分析 首先根据OA1、OB1分别是∠AOM和∠MOB的平分线,可得∠A1OB1=$\frac{1}{2}$α°;然后根据OA2、OB2分别是∠A1OM和∠MOB1的平分线,可得∠A2OB2=$\frac{1}{2}$∠A1OB1=$\frac{1}{2}×$$\frac{1}{2}$α°=$\frac{1}{{2}^{2}}$α°;再根据OA3、OB3分别是∠A2OM和∠MOB2的平分线,可得∠A3OB3=$\frac{1}{2}$∠A2OB2=$\frac{1}{2}×$$\frac{1}{{2}^{2}}$α°=$\frac{1}{{2}^{3}}$α°,…,据此判断出∠AnOBn=$\frac{1}{{2}^{n}}$α°即可.
解答 解:∵OA1、OB1分别是∠AOM和∠MOB的平分线,
∴∠A1OB1=$\frac{1}{2}$α°;
∵OA2、OB2分别是∠A1OM和∠MOB1的平分线,
∴∠A2OB2=$\frac{1}{2}$∠A1OB1=$\frac{1}{2}×$$\frac{1}{2}$α°=$\frac{1}{{2}^{2}}$α°;
∵OA3、OB3分别是∠A2OM和∠MOB2的平分线,
∴∠A3OB3=$\frac{1}{2}$∠A2OB2=$\frac{1}{2}×$$\frac{1}{{2}^{2}}$α°=$\frac{1}{{2}^{3}}$α°;
…,
∵OAn、OBn分别是∠An-1OM和∠MOBn-1的平分线,
则∠AnOBn=$\frac{1}{{2}^{n}}$α°.
故答案为:$\frac{1}{{2}^{n}}$α°.
点评 此题主要考查了角的计算,考查了分析推理能力,要熟练掌握,解答此题的关键是要明确角的平分线的性质:一个角的平分线把这个角分成两个大小相同的角.

 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案| A. | 8 | B. | 0 | C. | -1 | D. | -6 |
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 直方图 |
| A. | 调查该校全体女生 | |
| B. | 调查该校全体男生 | |
| C. | 调查该校七年级全体学生 | |
| D. | 调查该校七、八、九年级学生各100名 |
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=12cm,BC=18cm,点P从点A出发以2cm/s的速度沿A→D→C运动,点P从点A出发的同时点Q从点C出发,以1cm/s的速度向点B运动,当点P到达点C时,点Q也停止运动.设点P,Q运动的时间为t秒.