题目内容
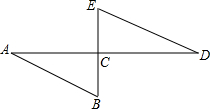 如图,AD⊥BE于点C,点C是BE的中点,AB=DE,
如图,AD⊥BE于点C,点C是BE的中点,AB=DE,求证:AB∥DE.
考点:全等三角形的判定与性质,平行线的判定
专题:证明题
分析:根据直角三角形的判定定理HL可得出Rt△ACB≌Rt△DCE,则∠B=∠E从而得出AB∥DE.
解答:证明:∵AD⊥BE,
∴∠ACB=∠DCE=90°,
∵C是BE的中点,
∴BC=EC,
在Rt△ACB和Rt△DCE中,
,
∴Rt△ACB≌Rt△DCE(HL),
∴∠B=∠E(全等三角形的对应角相等),
∴AB∥DE.
∴∠ACB=∠DCE=90°,
∵C是BE的中点,
∴BC=EC,
在Rt△ACB和Rt△DCE中,
|
∴Rt△ACB≌Rt△DCE(HL),
∴∠B=∠E(全等三角形的对应角相等),
∴AB∥DE.
点评:本题考查了全等三角形的判定和性质,以及平行线的判定,正确证明三角形全等是关键.

练习册系列答案
相关题目
下列不是代数式的是( )
| A、x+y | B、c=0 |
| C、m+n | D、999n+99m |
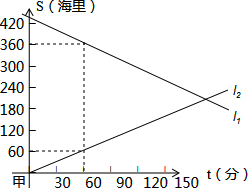 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.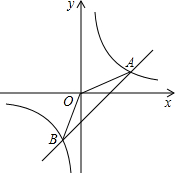 如图,已知A(4,a)、B(-2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(4,a)、B(-2,-4)是一次函数y=kx+b的图象和反比例函数y=