题目内容
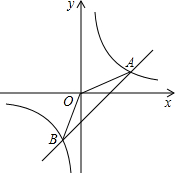 如图,已知A(4,a)、B(-2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(4,a)、B(-2,-4)是一次函数y=kx+b的图象和反比例函数y=| m |
| x |
(1)求反比例函数和一次函数的解析式;
(2)根据图象直接写出:当x取何值时,反比例函数的值大于一次函数的值;
(3)求△AOB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)A(4,a)、B(-2,-4)是一次函数y=kx+b的图象和反比例函数y=
的图象的交点,利用待定系数法,将点B(-2,-4)代入反比例函数关系式求出m的值,再将A的横坐标代入,求出A的纵坐标,然后将A、B点的坐标代入一次函数y=kx+b,组成二元一次方程组,求出一次函数的关系式;
(2)根据图象,观察反比例函数的值大于一次函数的值,从而确定x的取值范围;
(3)先求出一次函数与x轴交点C的坐标,再根据S△AOB=S△AOC+S△COB,计算即可求解.
| m |
| x |
(2)根据图象,观察反比例函数的值大于一次函数的值,从而确定x的取值范围;
(3)先求出一次函数与x轴交点C的坐标,再根据S△AOB=S△AOC+S△COB,计算即可求解.
解答:解:(1)把B(-2,-4)代入反比例函数y=
,
得到:-4=
,
解得m=8.
故所求反比例函数关系式为:y=
;
∵点A(4,a)在反比例函数的图象上
∴a=
=2,
∴点A的坐标为(4,2).
∵点A(4,2)和点B(2,4)都在一次函数y=kx+b的图象上,
∴
,
解得
.
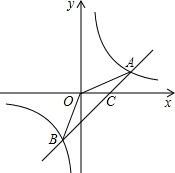 ∴一次函数的解析式为y=x-2;
∴一次函数的解析式为y=x-2;
(2)由图象可得,反比例函数的值大于一次函数的值的x的取值范围是:x<-2或0<x<4;
(3)设直线y=x-2与x轴相交于点C,
令y=0,得x=2,
则点C的坐标是(2,0),
所以S△AOB=S△AOC+S△COB=
×2×2+
×2×4=6.
| m |
| x |
得到:-4=
| m |
| -2 |
解得m=8.
故所求反比例函数关系式为:y=
| 8 |
| x |
∵点A(4,a)在反比例函数的图象上
∴a=
| 8 |
| 4 |
∴点A的坐标为(4,2).
∵点A(4,2)和点B(2,4)都在一次函数y=kx+b的图象上,
∴
|
解得
|
 ∴一次函数的解析式为y=x-2;
∴一次函数的解析式为y=x-2;(2)由图象可得,反比例函数的值大于一次函数的值的x的取值范围是:x<-2或0<x<4;
(3)设直线y=x-2与x轴相交于点C,
令y=0,得x=2,
则点C的坐标是(2,0),
所以S△AOB=S△AOC+S△COB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点,主要熟练掌握用待定系数法求函数的解析式.掌握数形结合的思想.

练习册系列答案
相关题目
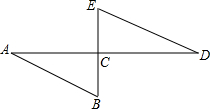 如图,AD⊥BE于点C,点C是BE的中点,AB=DE,
如图,AD⊥BE于点C,点C是BE的中点,AB=DE, 如图,已知EF∥BC,AE=3,BE=4,FC=6,则AF的值为
如图,已知EF∥BC,AE=3,BE=4,FC=6,则AF的值为 如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示)
如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示) 如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过点C作⊙O的切线交OD的延长线于点E,交AB的延长线于点F,连接EA.
如图,AB为⊙O的直径,C为⊙O上一点,D为AC的中点,过点C作⊙O的切线交OD的延长线于点E,交AB的延长线于点F,连接EA. 如图所示,直线EF过长方形ABCD的对称中心,交AD于点F,交BC于点E,若BE=2CE,求证:BF=EF.
如图所示,直线EF过长方形ABCD的对称中心,交AD于点F,交BC于点E,若BE=2CE,求证:BF=EF.