题目内容
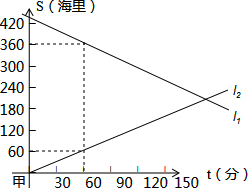 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船s与t的关系.(1)A、B两船的速度各是多少?
(2)分别写出两船到甲港距离s与行驶时间t的函数关系式;
(3)航行多长时间后,A、B两船相遇?
考点:一次函数的应用
专题:
分析:(1)分别根据60分钟的行驶路程列式计算即可得解;
(2)根据正比例函数解析式写出A船l2的解析式,再利用待定系数法求一次函数解析式求出B船l2的解析式;
(3)联立两函数解析式,解方程组即可得解.
(2)根据正比例函数解析式写出A船l2的解析式,再利用待定系数法求一次函数解析式求出B船l2的解析式;
(3)联立两函数解析式,解方程组即可得解.
解答:解:(1)A船速度:60÷60=1海里/分,
B船速度:(450-360)÷60=1.5海里/分;
(2)A的关系式为s=t,
设B的关系式为s=kt+b,
∵函数图象经过点(0,450),(60,360),
∴
,
解得
.
所以,s=-1.5t+450;
(3)联立
,
解得
.
答:航行180分钟后,A、B两船相遇.
B船速度:(450-360)÷60=1.5海里/分;
(2)A的关系式为s=t,
设B的关系式为s=kt+b,
∵函数图象经过点(0,450),(60,360),
∴
|
解得
|
所以,s=-1.5t+450;
(3)联立
|
解得
|
答:航行180分钟后,A、B两船相遇.
点评:本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,时间、路程、速度三者之间的关系,准确识图获取信息是解题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
如果+10表示“增加10”,那么“减少8”可以记作( )
| A、-18 | B、-8 | C、+2 | D、+8 |
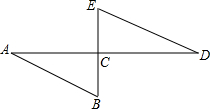 如图,AD⊥BE于点C,点C是BE的中点,AB=DE,
如图,AD⊥BE于点C,点C是BE的中点,AB=DE,
 如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示)
如图,∠AOB=164°59′58″,∠AOC=∠BOD=90°,求∠COD的度数(结果用度,分,秒表示)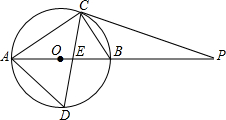 如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE
如图,⊙O的直径AB为10,弦BC为6,D、E分别是∠ACB的平分线与⊙O,AB的交点,P为AB延长线上一点,且PC=PE