题目内容
2. 如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①③⑤(写出所有正确结论的序号).
如图,边长为4的正方形ABCD中,P是BC边上一动点(不含B、C点).将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有①③⑤(写出所有正确结论的序号).①∠NAP=45°;
②当P为BC中点时,AE为线段NP的中垂线;
③四边形AMCB的面积最大值为10;
④线段AM的最小值为2$\sqrt{5}$;
⑤当△ABP≌△ADN时,BP=4$\sqrt{2}$-4.
分析 ①正确,先判断出Rt△APE≌Rt△APB,即可得出结论;
②错误,设ND=NE=y,在Rt△PCN中,利用勾股定理求出y即可解决问题.
③正确,设PB=x,构建二次函数,利用二次函数性质解决问题即可.
④错误,作MG⊥AB于G,因为AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\sqrt{16+A{G}^{2}}$,所以AG最小时AM最小,构建二次函数,求得AG的最小值为3,AM的最小值为5.
⑤正确,在AB上取一点K使得AK=PK,列出关于PB的方程即可解决问题.
解答 解: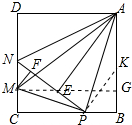 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴∠D=∠B=∠BAD=90°,AD=AB,
由折叠知,∠DAN=∠EAN,∠AEN=∠ADN=90°,AE=AD
∴AE=AB,
在Rt△APE和Rt△APB中,$\left\{\begin{array}{l}{AP=AP}\\{AE=AB}\end{array}\right.$,
∴Rt△APE≌Rt△APB,
∴∠EAP=∠BAP,
∵∠DAN=∠EAN,∠BAD=90°,
∴∠PAN=45°,
故①正确,
当PB=PC=PE=2时,
由折叠知,ND=NE,
设ND=NE=y,
在Rt△PCN中,(y+2)2=(4-y)2+22解得y=$\frac{4}{3}$,
∴NE≠EP,故②错误,
设PB=x,则CP=4-x,
∵△CMP∽△BPA,
∴$\frac{PB}{CM}=\frac{AB}{PC}$,
∴CM=$\frac{1}{4}$x(4-x),
∴S四边形AMCB=$\frac{1}{2}$[4+$\frac{1}{4}$x(4-x)]×4=-$\frac{1}{2}$x2+2x+8=-$\frac{1}{2}$(x-2)2+10,
∴x=2时,四边形AMCB面积最大值为10,故③正确,
作MG⊥AB于G,
∵AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\sqrt{16+A{G}^{2}}$,
∴AG最小时AM最小,
∵AG=AB-BG=AB-CM=4-$\frac{1}{4}$x(4-x)=$\frac{1}{4}$(x-2)2+3,
∴x=2时,AG最小值=3,
∴AM的最小值=$\sqrt{16+9}$=5,故④错误.
∵△ABP≌△ADN时,
∴∠PAB=∠DAN=22.5°,在AB上取一点K使得AK=PK,
∴∠KPA=∠KAP=22.5°
∵∠PKB=∠KPA+∠KAP=45°,
∴∠BPK=∠BKP=45°,
∴PB=BK,AK=PK=$\sqrt{2}$PB,
∴PB+$\sqrt{2}$PB=4,
∴PB=4$\sqrt{2}$-4,故⑤正确.
故答案为:①③⑤.
点评 此题是四边形综合题主要考查了正方形的性质、相似三角形的判定和性质、全等三角形的性质、勾股定理等知识,解题的关键是学会构建二次函数解决最值问题,学会添加常用辅助线,属于中考压轴题.

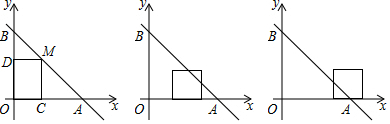
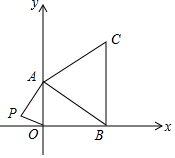 如图所示,在直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.
如图所示,在直角坐标系中,已知A(0,a)、B(b,0)、C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,(c-4)2≤0.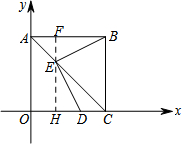 探索与发现
探索与发现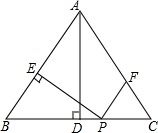 如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.
如图,在等腰△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,动点P从点B出发沿BC方向以每秒5个单位的速度向终点C运动,过点P作PE⊥AB于点E,过点P作PF∥BA,交AC于点F,设点P运动的时间为t秒.若以PE所在的直线为对称轴,线段BD经轴对称变换后的图形为B'D',求当线段B'D'与线段AC有交点这段过程中,线段B'D'扫过的面积$\frac{66}{25}$.