题目内容
1.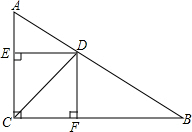 如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.
如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.
分析 先证明四边形DECF是矩形,再由角平分线的性质得出DE=DF,即可得出结论.
解答 证明:∵CD是角平分线,DE⊥AC,DF⊥BC,
∴DE=DF,∠CED=∠CFD=90°,
∵∠ACB=90°,
∴四边形DECF是矩形,
又∵DE=DF,
∴四边形DECF是正方形.
点评 本题考查了正方形的判定方法、矩形的判定方法、角平分线的性质;熟练掌握正方形的判定方法,证明四边形是矩形是解决问题的关键,难度适中.

练习册系列答案
相关题目
9.抛物线y=x2-bx(b≠0)的顶点为C,与x轴交于A、B两点,且△ABC是等腰直角三角形,则S△ABC为( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
16.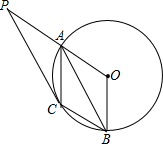 如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
(1)求证:四边形OACB是菱形;
(2)延长OA至P使得0A=AP,连接PC,求证:PC是⊙O的切线.
 如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点. (1)求证:四边形OACB是菱形;
(2)延长OA至P使得0A=AP,连接PC,求证:PC是⊙O的切线.
11.下列说法中,正确的是( )
| A. | 一个轴对称图形一定只有一条对称轴 | |
| B. | 全等三角形一定是关于某直线对称的 | |
| C. | 两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧 | |
| D. | 两个图形关于某直线对称,则这两个图形对应点所连线段一定被这条直线垂直平分 |
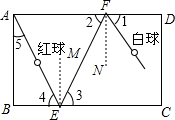 如图,选择适当的方向击打白球,可使白球经过两次反弹后将红球撞入底袋,白球在运动过程中,∠1=∠2,∠3=∠4,如果红球与洞口的连线与台球桌边缘的夹角∠5=25°,那么选择∠1是多少度,才能保证红球能直接入袋?为什么?
如图,选择适当的方向击打白球,可使白球经过两次反弹后将红球撞入底袋,白球在运动过程中,∠1=∠2,∠3=∠4,如果红球与洞口的连线与台球桌边缘的夹角∠5=25°,那么选择∠1是多少度,才能保证红球能直接入袋?为什么?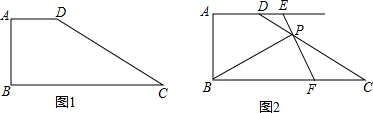
 如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积.
如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积.