题目内容
12.已知二次函数y=-$\frac{1}{2}$x2+3x-2.(1)用配方法求该抛物线的对称轴,并说明:当x取何值时,y的值随x值的增大而减小?
(2)将二次函数y=-$\frac{1}{2}$x2的图象经过怎样的平移能得到y=-$\frac{1}{2}$x2+3x-2的图象?
分析 (1)可通过将二次函数y=-$\frac{1}{2}$x2+3x-2化为顶点式,再依次判断对称轴、顶点坐标、开口方向及函数增减性等问题.
(2)将函数y=-$\frac{1}{2}$x2+3x-2化为y=-$\frac{1}{2}$(x-3)2+$\frac{5}{2}$,将二次函数y=-$\frac{1}{2}$x2的图象经过平移能得到y=-$\frac{1}{2}$(x-3)2+$\frac{5}{2}$的图象,x需减3,y需加$\frac{5}{2}$,在x轴方向上移动时减为向右移动,在y轴方向上移动时加为向上移动.
解答 解:(1)把抛物线y=-$\frac{1}{2}$x2+3x-2化为顶点坐标式为y=-$\frac{1}{2}$x2+3x-2=-$\frac{1}{2}$(x-3)2+$\frac{5}{2}$,
故对称轴为x=3,当x>3时,y随x的增大而减小.
(2)函数数y=-$\frac{1}{2}$x2的图象先向上平移$\frac{5}{2}$个单位,再向右平移3个单位,得到函数y=-$\frac{1}{2}$x2+3x-2的图象.
点评 本题主要考查二次函数的性质,解答本题的关键是把抛物线的一般形式转化成顶点坐标式,此题比较简单.

练习册系列答案
相关题目
20.下列说法中正确的是( )
| A. | 带根号的数都是无理数 | B. | 不带根号的数一定是有理数 | ||
| C. | 无限小数都是无理数 | D. | 无理数是无限小数 |
4.在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{1}{2}$,则S△ABC=( )
| A. | 30 | B. | 40 | C. | 10$\sqrt{5}$ | D. | 20 |
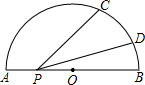 如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.
如图,半圆的直径AB=4,P是AB上一动点,C、D在半圆上,$\widehat{BC}$、$\widehat{BD}$的度数分别是75°和15°,则PC+PD的最小值为2$\sqrt{2}$.

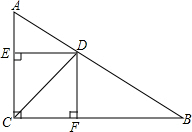 如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.
如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.