题目内容
16.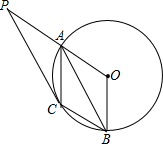 如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点.
如图,A、B是⊙O上的两点,∠A0B=120°,C是$\widehat{AB}$的中点. (1)求证:四边形OACB是菱形;
(2)延长OA至P使得0A=AP,连接PC,求证:PC是⊙O的切线.
分析 (1)连结OC,由C是$\widehat{AB}$的中点,∠AOB=l20°,根据在同圆或等圆中,相等的弧所对的圆心角相等得到∠AOC=∠BOC=60°,易得△OAC和△OBC都是等边三角形,则AC=OA=OB=BC,根据菱形的判定方法即可得到结论.
(2)欲证明PC是⊙O的切线,只需推知PC⊥OC即可.
解答 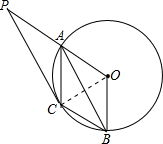 证明:(1)连结OC,如图,
证明:(1)连结OC,如图,
∵C是$\widehat{AB}$的中点,∠AOB=l20°,
∴∠AOC=∠BOC=60°,
又∵OA=OC=OB,
∴△OAC和△OBC都是等边三角形,
∴AC=OA=OB=BC,
∴四边形OACB是菱形.
(2)∵由(1)知,△OAC是等边三角形,
∴AC=OA,∠OAC=∠ACO=60°,
∴∠PAC=120°.
又∵0A=AP,
∴AP=AC,
∴∠APC=∠ACP=30°,
∴∠PCO=∠PCA+∠ACO=90°,
即PC⊥OC.
又∵OC是半径,
∴PC是⊙O的切线.
点评 本题考查了圆心角、弧、弦的关系:在同圆或等圆中,相等的弧所对的圆心角相等.也考查了等边三角形的判定与性质以及菱形的判定.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
4.在Rt△ABC中,∠C=90°,AB=10,tanB=$\frac{1}{2}$,则S△ABC=( )
| A. | 30 | B. | 40 | C. | 10$\sqrt{5}$ | D. | 20 |
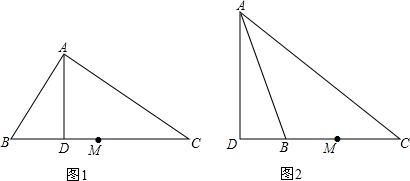

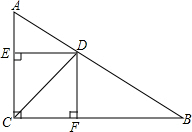 如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.
如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.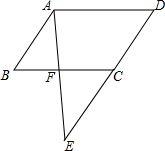 已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求:
已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求: