题目内容
10. 如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积.
如图,已知抛物线y=-x2+2x+1交x轴于A、B点,交y轴于C点,直线l过点C,D(-1,0)两点且交抛物线于P点,求四边形ABPC的面积.
分析 根据抛物线解析式求得点A、B、C的坐标,由点C、D的坐标得到直线CD的解析式,联合直线与抛物线方程求得点P的坐标,则四边形ABPC的面积=△ABP的面积-△ACD的面积.
解答 解:由y=-x2+2x+1得到:A(1-$\sqrt{2}$,0),B(1+$\sqrt{2}$,0),C(0,1).
设直线CD的解析式为:y=kx+b(k≠0).
把C(0,1),D(-1,0)代入,得
$\left\{\begin{array}{l}{b=1}\\{-k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
则直线CD的解析式为:y=x+1.
所以$\left\{\begin{array}{l}{y=-{x}^{2}+2x+1}\\{y=x+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
则点P的坐标是(0,1)(舍去,与点C重合)或(1,2).
∴S四边形ABPC=S△ADP-S△ACD=$\frac{1}{2}$(2+$\sqrt{2}$)×2-$\frac{1}{2}$×$\sqrt{2}$×1=2+$\frac{\sqrt{2}}{2}$,即四边形ABPC的面积是2+$\frac{\sqrt{2}}{2}$.
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题可转化为解关于x的一元二次方程.也考查了二次函数的性质和二次函数与一次函数图象的交点问题.运用数形结合的思想是解决本题的关键.

| A. | 带根号的数都是无理数 | B. | 不带根号的数一定是有理数 | ||
| C. | 无限小数都是无理数 | D. | 无理数是无限小数 |
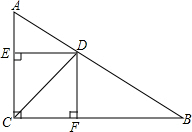 如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.
如图,在△ABC中,∠ACB=90°,CD是角平分线,DE⊥AC,DF⊥BC,垂足分别是E,F.求证:四边形DECF是正方形.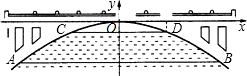 有一座抛物线形拱桥,如图所示,桥下面在正常水位时AB宽为20m,此时拱顶到水面的距离为4m,水位警戒线CD宽为10m.
有一座抛物线形拱桥,如图所示,桥下面在正常水位时AB宽为20m,此时拱顶到水面的距离为4m,水位警戒线CD宽为10m.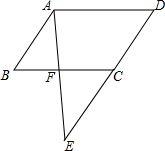 已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求:
已知四边形ABCD为平行四边形,F在BC上,E在DC的延长线上,且AF:EF=2:3.求: 如图.矩形ABCD的顶点B,C在坐标轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.
如图.矩形ABCD的顶点B,C在坐标轴上,顶点D的坐标是(3,3),若直线y=mx恰好将矩形分成面积相等的两部分,求m的值.