题目内容
4.解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1-3(x-1)<8-x}\end{array}\right.$,并写出该不等式组的整数解.分析 分别求出各不等式的解集,再求出其公共解集,在其公共解集内找出x的整数解即可.
解答 解:$\left\{\begin{array}{l}{\frac{x-3}{2}≥x+1①}\\{1-3(x-1)<8-x②}\end{array}\right.$,
由①得,x≤1;
由②得,x>-2,
故此不等式的解集为:-2<x≤1,其整数解为:-1,0,1.
点评 本题考查的是解一元一次不等式组及不等式组的整数解,熟知同大取大;同小取小;大小小大中间找;大大小小找不到的规律是解答此题的关键.

练习册系列答案
相关题目
15.若一直角三角形两边长为4和5,则第三边长为( )
| A. | 3 | B. | $\sqrt{41}$ | C. | 3或$\sqrt{41}$ | D. | 不确定 |
19. 如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
 如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )
如图是一块长方形ABCD的场地,长AB=102m,宽AD=51m,从A、B两处入口的中路宽都为1m,两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为( )| A. | 5050m2 | B. | 5000m2 | C. | 4900m2 | D. | 4998m2 |
16. 如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
 如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )
如图,⊙O的直径AB=8,∠CBD=30°,则CD等于( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
14.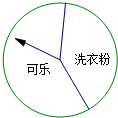 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
(1)完成上述表格;(结果全部精确到0.1)
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘.商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 604 | |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.59 | 0.604 |
(2)请估计当n很大时,频率将会接近0.6,假如你去转动该转盘一次,你获得“可乐”的概率约是0.6;(结果全部精确到0.1)
(3)转盘中,表示“洗衣粉”区域的扇形的圆心角约是多少度?
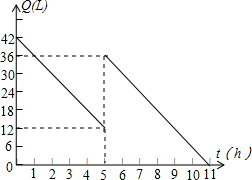 某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题:
某机动车出发前油箱内有油42L,行驶若干小时后,在途中加油站加油若干升.油箱中余油量Q(L)与行驶时间t(h)之间的函数关系如图所示,根据如图回答问题: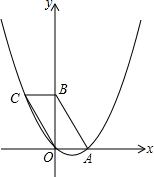 已知,如图,把平行四边形OABC放置于平面直角坐标系中,OA落在x轴的正半轴上,OB落在y轴的正半轴上,OA=2,OB=4,抛物线y=ax2+bx+c经过A、O、C三点.
已知,如图,把平行四边形OABC放置于平面直角坐标系中,OA落在x轴的正半轴上,OB落在y轴的正半轴上,OA=2,OB=4,抛物线y=ax2+bx+c经过A、O、C三点.