题目内容
13.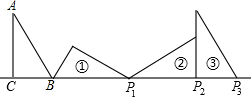 如图,Rt△ABC中,∠ACB=90°,AC=1,∠A=30°,且BC边在直线a上,将△ABC绕点B顺时针旋转到位置①可得到点P1,此时BP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时BP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时BP3=3+$\sqrt{3}$;…,按此规律继续旋转,直至得到点P2015为止.则BP2015=2015+672$\sqrt{3}$.
如图,Rt△ABC中,∠ACB=90°,AC=1,∠A=30°,且BC边在直线a上,将△ABC绕点B顺时针旋转到位置①可得到点P1,此时BP1=2;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时BP2=2+$\sqrt{3}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时BP3=3+$\sqrt{3}$;…,按此规律继续旋转,直至得到点P2015为止.则BP2015=2015+672$\sqrt{3}$.
分析 观察不难发现,每旋转3次为一个循环组依次循环,用2013除以3求出循环组数,然后列式计算即可得解.
解答 解:由图可知,每旋转3次为一个循环组依次循环,
∵2015÷3=671…2,
∴AP2015为671个循环组的长度+BP2,
∵BP3=3+$\sqrt{3}$,
∴BP2015=671×(3+$\sqrt{3}$)+2+$\sqrt{3}$=2015+672$\sqrt{3}$,
故答案为:2015+672$\sqrt{3}$.
点评 本题考查了旋转的性质,读懂题目信息并仔细观察图形得到每旋转3次为一个循环组依次循环是解题的关键.

练习册系列答案
相关题目
2.sin60°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
3.下列运算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=-3 | B. | a2•a4=a6 | C. | (2a2)3=2a6 | D. | (a+2)2=a2+4 |
 如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?
如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?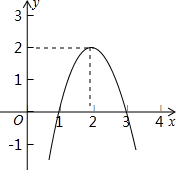 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2.
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象可知:方程ax2+bx+c=k有两个不相等的实数根,则k的取值范围为k<2. 甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )
甲乙两车分别从M,N两地相向而行,甲车出发1小时后乙车出发,并以各自的速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的路程S(千米)与甲车所用时间t(小时)之间的函数图象,其中D点表示甲车到达B地停止行驶.下列说法:①A,B两地路程是560千米;②乙车的速度是100千米/小时;③a=$\frac{1100}{3}$;④乙车出发3小时与甲车相遇,其中正确的个数为( )