题目内容
3．
如图，小明把△ABC纸片沿DE折叠，当点A落在四边形BCDE内部时，他发现2∠A=∠1+∠2，你能帮他解释其中的原因吗？
分析 如图，连接AA′，先根据折叠的性质得到∠A=∠A′，再根据三角形外角性质得∠1=∠EAA′+∠EA′A，∠2=∠DAA′+∠DA′A，然后把两式相加即可得到2∠A=∠1+∠2．
解答 解：
如图，连接AA′，
∵△ABC纸片沿DE折叠，当点A落在四边形BCDE内部，
∴∠A=∠A′，
∵∠1=∠EAA′+∠EA′A，∠2=∠DAA′+∠DA′A，
∴∠1+∠2=∠EAA′+∠EA′A+∠DAA′+∠DA′A=∠A+∠A′=2∠A，
即2∠A=∠1+∠2．
点评 本题考查了三角形内角和定理：三角形内角和是180°．主要用在求三角形中角的度数：①直接根据两已知角求第三个角；②依据三角形中角的关系，用代数方法求三个角；③在直角三角形中，已知一锐角可利用两锐角互余求另一锐角．也考查了折叠的性质．
练习册系列答案
相关题目
将一直角三角板与两边平行的纸条（如图所示放置），给出下列结论：①∠1=∠2；②∠3=∠4；③∠4+∠2=180°；④∠5+∠4=180°．其中正确的个数是（ ）
11．
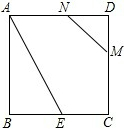如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（ ）时，△ABE与以D、M、N为顶点的三角形相似．
如图，正方形ABCD的边长为2，BE=CE，MN=1，线段MN的两端点在CD、AD上滑动，当DM为（ ）时，△ABE与以D、M、N为顶点的三角形相似．| A． | $\frac{{\sqrt{5}}}{5}$ | B． | $\frac{{2\sqrt{5}}}{5}$ | C． | $\frac{{\sqrt{5}}}{5}$或$\frac{{2\sqrt{5}}}{5}$ | D． | $\frac{{2\sqrt{5}}}{5}$或$\frac{{3\sqrt{5}}}{5}$ |
如图，在平行四边形ABCD中，已知M和N分别是边AB、DC的中点，试说明四边形BMDN也是平行四边形．
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连结AG、CF．下列结论中正确结论的个数是（ ）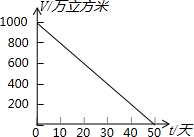
2007年的夏天，湖南省由于持续高温和连日无雨，水库蓄水量普遍下降，如图是某水库的蓄水量V（万立方米）与干旱持续时间t（天）之间的关系图，请根据此图，回答下列问题：
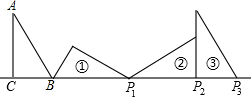如图，Rt△ABC中，∠ACB=90°，AC=1，∠A=30°，且BC边在直线a上，将△ABC绕点B顺时针旋转到位置①可得到点P1，此时BP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时BP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时BP3=3+$\sqrt{3}$；…，按此规律继续旋转，直至得到点P2015为止．则BP2015=2015+672$\sqrt{3}$．