题目内容
18．
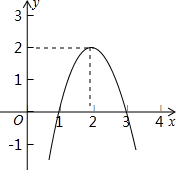二次函数y=ax2+bx+c（a≠0）的图象如图所示，根据图象可知：方程ax2+bx+c=k有两个不相等的实数根，则k的取值范围为k＜2．
分析 先由交点式求出二次函数的解析式，再由方程的根的情况得出判别式△＞0，解不等式即可得出k的取值范围．
解答 解：根据题意得：二次函数的图象与x轴的交点为：（1，0）、（3，0），
设二次函数y=a（x-1）（x-3），
把点（2，2）代入得：a=-2，
∴二次函数的解析式为：y=-2（x-1）（x-3）
即y=-2x2+8x-6；
∵方程-2x2+8x-6=k有两个不相等的实数根，
∴-2x2+8x-6-k=0，
△=82-4×（-2）×（-6-k）＞0，
解得：k＜2；
故答案为：k＜2．
点评 本题考查了抛物线与x轴的交点、二次函数解析式的求法、不等式的解法；熟练掌握二次函数图象的有关性质，并能进行推理计算是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，在平行四边形ABCD中，已知M和N分别是边AB、DC的中点，试说明四边形BMDN也是平行四边形．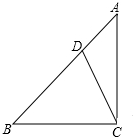
如图，在△ABC中，∠ACB=90°，AC=BC，点D在边AB上，连接CD，
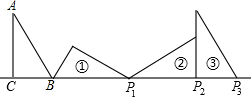如图，Rt△ABC中，∠ACB=90°，AC=1，∠A=30°，且BC边在直线a上，将△ABC绕点B顺时针旋转到位置①可得到点P1，此时BP1=2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时BP2=2+$\sqrt{3}$；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时BP3=3+$\sqrt{3}$；…，按此规律继续旋转，直至得到点P2015为止．则BP2015=2015+672$\sqrt{3}$．
如图，一次函数y=x-2图象与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点A（3，m），与x轴交于点B．
7．在⊙O中，圆心O到弦AB的距离为AB长度的一半，则弦AB所对圆心角的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |