题目内容
4.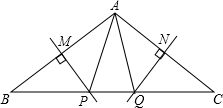 如图,在△ABC中,∠BAC=105°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
如图,在△ABC中,∠BAC=105°,若MP和NQ分别垂直平分AB和AC,求∠PAQ的度数.
分析 先根据三角形内角和等于180°求出∠ABP+∠ACQ=75°,再根据线段垂直平分线的性质∠PAB=∠ABP,∠QAC=∠ACQ,所以∠PAB+∠QAC=75°,便不难求出∠PAQ的度数为30°.
解答 解:∵∠BAC=105°,
∴∠ABP+∠ACQ=180°-105°=75°,
∵MP、NQ分别垂直平分AB和AC,
∴PB=PA,QC=QA.
∴∠PAB=∠ABP,∠QAC=∠ACQ,
∴∠PAB+∠QAC=∠ABP+∠ACQ=75°,
∴∠PAQ=105°-75°=30°.
点评 本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上的点到线段两端的距离相等是解答此题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
17.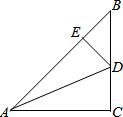 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,且AB=10cm,则△BED的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,且AB=10cm,则△BED的周长为( )
 如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,且AB=10cm,则△BED的周长为( )
如图,△ABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于点D,DE⊥AB,且AB=10cm,则△BED的周长为( )| A. | 5 cm | B. | 10 cm | C. | 15 cm | D. | 20 cm |
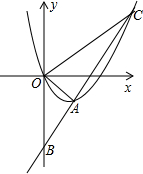 如图,已知抛物线y=x2-2x的顶点为A,直线y=2x+b经过点A,且交y轴于点B,O为坐标原点.
如图,已知抛物线y=x2-2x的顶点为A,直线y=2x+b经过点A,且交y轴于点B,O为坐标原点.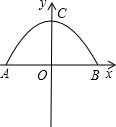 如图,拱桥呈抛物线形,其函数关系式为y=-$\frac{1}{4}$x2+h,当拱桥下水位线在AB位置时,水面宽为12米:
如图,拱桥呈抛物线形,其函数关系式为y=-$\frac{1}{4}$x2+h,当拱桥下水位线在AB位置时,水面宽为12米: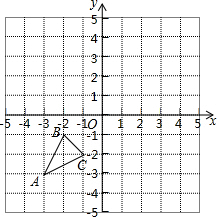 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是直角坐标平面上三点.