题目内容
 如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为
如图,在△ABC中,AD是BC边上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F.若△ABC的面积为3,则四边形EFDC的面积为考点:三角形的面积
专题:
分析:连接CF,根据CE=2AE,△ABC的面积为3可知S△ABE=
×3=1,S△CEF=
×3=2,S△AEF:S△CEF=1:2,设S△AEF=S,则S△CEF=2S故S△AEF=1-S,则S△BCF=2-2S,设S△AEF=x=1-S,则S△BCF=2x=2-2S,由AD是BC边上的中线可知S△BDF=S△CDF=x,2x=x+3S,即x=3S,所以S△ABC=12S,S四边形EFDC=5S,由此可得出结论.
| 1 |
| 3 |
| 2 |
| 3 |
解答: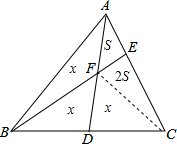 解:连接CF,
解:连接CF,
∵CE=2AE,△ABC的面积为3,
∴S△ABE=
×3=1,S△CEF=
×3=2,
S△AEF:S△CEF=1:2,
设S△AEF=S,则S△CEF=2S,
∴S△AEF=1-S,则S△BCF=2-2S,
设S△AEF=x=1-S,则S△BCF=2x=2-2S,
∵AD是BC边上的中线,
∴S△BDF=S△CDF=x,2x=x+3S,即x=3S,
∴S△ABC=12S,S四边形EFDC=5S,
∴
=
=
.
∴S四边形EFDC=
=
.
故答案为:
.
 解:连接CF,
解:连接CF,∵CE=2AE,△ABC的面积为3,
∴S△ABE=
| 1 |
| 3 |
| 2 |
| 3 |
S△AEF:S△CEF=1:2,
设S△AEF=S,则S△CEF=2S,
∴S△AEF=1-S,则S△BCF=2-2S,
设S△AEF=x=1-S,则S△BCF=2x=2-2S,
∵AD是BC边上的中线,
∴S△BDF=S△CDF=x,2x=x+3S,即x=3S,
∴S△ABC=12S,S四边形EFDC=5S,
∴
| S△ABC |
| S四边形EFDC |
| 12S |
| 5S |
| 12 |
| 5 |
∴S四边形EFDC=
| 15 |
| 12 |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查的是三角形的面积,熟知三角形的面积公式是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 下图右边四个图形中是左边展开图的立体图的是( )
下图右边四个图形中是左边展开图的立体图的是( )A、 |
B、 |
C、 |
D、 |
三元一次方程组
的解为( )
|
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
下列说法正确的是( )
| A、为了解全市中学生的睡眠状况,宜采用普查方式 |
| B、某地会发生地震是必然事件 |
| C、某校教师150人,其中31岁~35岁组的频率为0.2,那么在该段的教师有30人 |
| D、若甲组数据的方差S甲2=0.1,乙组数据的方差S乙2=0.2,则乙组数据比甲组稳定 |
在等式y=kx+b中,当x=1时,y=2;当x=2时,y=-4,则式子3k+2b的值为( )
| A、-34 | B、-2 | C、34 | D、2 |
 如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是
如图,在平行四边形ABCD中,∠ABC的平分线BE与AD交于点E,且ED=2AE,AE=3,则平行四边形ABCD的周长是