题目内容
19.已知梯形ABCD中,AD∥BC,则∠A:∠B:∠C:∠D不可能是( )| A. | 3:7:5:5 | B. | 5:4:5:4 | C. | 4:5:6:3 | D. | 8:1:4:5 |
分析 由梯形的性质得出同旁内角互补,得出A、C、D有可能;由平行四边形的判定方法得出B不可能.
解答 解: ∵AD∥BC,
∵AD∥BC,
∴∠A+∠B=180°,∠C+∠D=180°,
即∠A+∠B=∠C+∠D,
∴A、C、D选项有可能;
B选项不可能;
∵若∠A:∠B:∠C:∠D=5:4:5:4,
则∠A=∠C,∠B=∠D,
则四边形ABCD是平行四边形,
∴B不可能.
故选:B.
点评 本题考查了梯形的性质、平行四边形的判定方法;熟练掌握梯形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
9.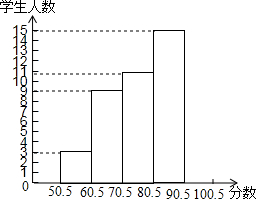 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
(1)根据以上信息,统计表中A=0.18,B=12,C=0.24;
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 3 | 0.06 |
| 60.5~70.5 | 9 | A |
| 70.5~80.5 | 11 | 0.22 |
| 80.5~90.5 | 15 | 0.30 |
| 90.5~100.5 | B | C |
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
7.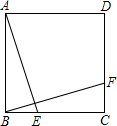 如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )
 如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,且BE=CF,连接AE,BF,将△ABE绕正方形的中心按逆时针方向旋转α(0<α<180°)到∠BCF,则旋转角α等于( )| A. | 90° | B. | 60° | C. | 45° | D. | 120° |
4.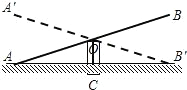 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )| A. | 40° | B. | 60° | C. | 80° | D. | 20° |
11. 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
8.观察下列4个命题:
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
9.己知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的斜边上的高为( )
| A. | 12 | B. | 6 | C. | 5 | D. | $\frac{12}{5}$ |
 如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.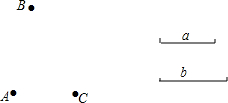 如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.
如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.