题目内容
5.将抛物线y=2x2-12x+19绕它的顶点旋转180°后的解析式是( )| A. | y=-2x2-12x+19 | B. | y=-2x2+12x-19 | C. | y=-2x2+12x-17 | D. | y=-2x2-12x-17 |
分析 根据配方法,可得顶点式解析式,根据旋转的性质,可得二次项的系数相同.
解答 解:y=2x2-12x+19化成顶点式为y=2(x-3)2+1,
将抛物线y=2x2-12x+19绕它的顶点旋转180°后的解析式是y=-2(x-3)2+1,
即y=-2x2+12x-17.
故选:C.
点评 本题考查了二次函数图象与几何变换,开口方向相反顶点相同是解题关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
15.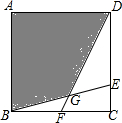 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
 如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )
如图,在正方形ABCD中,E在CD边上,F在BC边上,AB=1,DE=2CE,BF=FC,BE与DF交于点G,则图中阴影部分(即四边形ABGD)的面积是( )| A. | $\frac{9}{14}$ | B. | $\frac{2}{3}$ | C. | $\frac{7}{10}$ | D. | $\frac{3}{4}$ |
20.下列计算中,正确的是( )
| A. | x3•x2=x6 | B. | 3x2-2x2=x2 | C. | (x2)3=x5 | D. | $\sqrt{4}$=±2 |
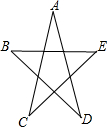 如图,∠A+∠B+∠C+∠D+∠E的度数是180°.
如图,∠A+∠B+∠C+∠D+∠E的度数是180°. 如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.
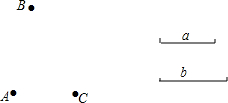 如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.
如图,已知平面上三个点A,B,C和线段a,b,按下列要求画图.