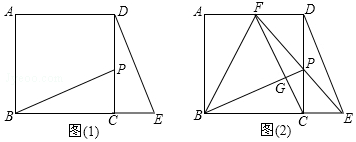
题目内容
20.(1)如图(1),点P是正方形ABCD的边CD上一点(点P与点C,D不重合),点E在BC的延长线上,且CE=CP,连接BP,DE.求证:BP=DE且BP⊥DE;(2)直线EP交AD于F,连接BF,FC.点G是FC与BP的交点.
①若BC=2CE时,求证:BP⊥CF;
②若BC=n•CE(n是大于1的实数)时,记△BPF的面积为S1,△DPE的面积为S2.求证:S1=(n+1)S2.
分析 (1)延长BP交DE于M,证明△BCP≌△DCE,根据全等三角形的性质证明即可;
(2)①根据等腰直角三角形的性质、正方形的性质证明△BCP≌△CDF,根据全等三角形的性质证明即可;
②设CE=CP=1,根据题意用n表示出BC、DP,根据梯形、三角形的面积公式计算即可.
解答 (1)证明:延长BP交DE于M,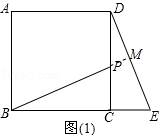
在△BCP和△DCE中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCP=∠DCE=90°}\\{CP=CE}\end{array}\right.$,
∴△BCP≌△DCE,
∴BP=DE,∠CBP=∠CDE,
∵∠CDE+∠E=90°,
∴∠CBP+∠E=90°,即BP⊥DE;
(2)①证明:∵CP=CE,∠PCE=90°,
∴∠CPE=45°,
∴∠FPD=∠CPE=45°,
∴∠PFD=45°,
∴FD=PD,
∵BC=2CE,
∴CD=2CE=2PC,即DP=CP,
∴DF=CP,
在△BCP和△CDF中,
$\left\{\begin{array}{l}{BC=CD}\\{∠BCP=∠CDF}\\{CP=DF}\end{array}\right.$,
∴△BCP≌△CDF,
∴∠FCD=∠CBP,
∵∠CBP+∠BPC=90°,
∴∠FCD+∠BPC=90°,即BP⊥CF;
②证明:设CE=CP=1,则BC=CD=n,DP=CD-CP=n-1,
∴FD=DP=n-1,
S1=S梯形BCDF-S△BCP-S△FDP
=$\frac{1}{2}$×(BC+DF)×CD-$\frac{1}{2}×$BC×CP-$\frac{1}{2}×$DF×FP
=$\frac{1}{2}×$(n+n-1)×n-$\frac{1}{2}×$n×1-$\frac{1}{2}×$(n-1)2
=$\frac{1}{2}$(n2-1)
=$\frac{1}{2}$(n+1)(n-1),
S2=$\frac{1}{2}×$DP×CE=$\frac{1}{2}$(n-1)×1=$\frac{1}{2}$(n-1),
∴S1=(n+1)S2.
点评 本题考查的是正方形的性质、全等三角形的判定和性质,掌握正方形的性质定理、全等三角形的判定定理和性质定理是解题的关键.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | 36.48(1+x)=43.25 | B. | 36.48(1+2x)=43.25 | C. | 36.48(1+x)2=43.25 | D. | 36.48(1-x)2=43.25 |
| A. | 540° | B. | 720° | C. | 900° | D. | 1080° |
| A. | 调查乘坐飞机的旅客是否携带了违禁物品 | |
| B. | 调查2017年央视春晚的全国收视率 | |
| C. | 调查某品牌日光灯的使用寿命 | |
| D. | 调查市场上营养快线的质量 |
 如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.
如图,函数y=ax+4和y=bx的图象相交于点A,则不等式bx≥ax+4的解集为x≥2.