题目内容
 如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.
如图,在△ABC中,∠B=90°,点P从点A开始沿AB边向点B以1cm/秒的速度移动,点Q从点B开始沿BC边向点C以2cm/秒的速度移动.(1)如果P、Q分别从A、B同时出发,几秒后△PBQ是等腰直角三角形?
(2)如果P、Q分别从A、B同时出发,几秒后△PBQ的面积等于3cm2?
(3)如果P、Q分别从A、B同时出发,四边形APQC的面积是△ABC面积的三分之二?
考点:一元二次方程的应用,等腰三角形的判定与性质
专题:几何动点问题
分析:(1)使△PQB为等腰三角形,则应有PB=BQ,就应有BA-AP=BQ,故设x秒后△PQB为等腰三角形,有PB=6-x=2x=BQ,解方程后可求解.
(2)设P,Q分别从A,B同时出发,y秒后,此时,AP=ycm,PB=(6-y)cm,BQ=2ycm,S△PBQ=
×PB×BQ,然后根据已知条件可列出方程,求出答案即可.
(3)此题实际上是求P、Q分别从A、B同时出发,几秒后△PBQ的面积等于8cm2.解法同(2).
(2)设P,Q分别从A,B同时出发,y秒后,此时,AP=ycm,PB=(6-y)cm,BQ=2ycm,S△PBQ=
| 1 |
| 2 |
(3)此题实际上是求P、Q分别从A、B同时出发,几秒后△PBQ的面积等于8cm2.解法同(2).
解答:解:(1)设x秒后△PQB为等腰直角三角形,
由题意得6-x=2x
解得x=2.
答:经过2秒△PQB为等腰三角形.
(2)设P,Q分别从A,B同时出发,y秒后△PBQ面积为3cm2,
则
•(6-y)•2y=3,
解得y1=3+
(不合题意,舍去),y2=3-
,
所以P,Q分别从A,B同时出发,3-
秒后△PBQ面积为3cm2;
(3)S△ABC=
×6×8=24(cm2).
∵四边形APQC的面积是△ABC面积的三分之二,
∴△PBQ的面积等于△ABC面积的三分之一.
设设P,Q分别从A,B同时出发,z秒后△PBQ面积为8cm2,
则
•(6-z)•2z=8,
解得z1=2,z2=4,
经检验,z1=2,z2=4均符合题意.
所以P,Q分别从A,B同时出发,2秒或4秒后四边形APQC的面积是△ABC面积的三分之二.
由题意得6-x=2x
解得x=2.
答:经过2秒△PQB为等腰三角形.
(2)设P,Q分别从A,B同时出发,y秒后△PBQ面积为3cm2,
则
| 1 |
| 2 |
解得y1=3+
| 6 |
| 6 |
所以P,Q分别从A,B同时出发,3-
| 6 |
(3)S△ABC=
| 1 |
| 2 |
∵四边形APQC的面积是△ABC面积的三分之二,
∴△PBQ的面积等于△ABC面积的三分之一.
设设P,Q分别从A,B同时出发,z秒后△PBQ面积为8cm2,
则
| 1 |
| 2 |
解得z1=2,z2=4,
经检验,z1=2,z2=4均符合题意.
所以P,Q分别从A,B同时出发,2秒或4秒后四边形APQC的面积是△ABC面积的三分之二.
点评:本题考查了等腰三角形的判定;通过列方程求解是正确解答本题的关键.此题首先把PB,PQ用含x(y、z)代数式表示,然后利用三角形面积公式即可列方程求解.但应注意考虑解的合理性,即考虑解的取舍.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
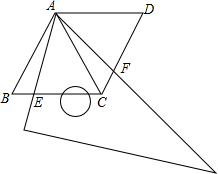 用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,如果使三角尺60°角的顶点与点A重合,两边分别与AB、AC重合,将三角尺绕A点按逆时针方向旋转.如图,三角尺的两边分别与菱形的两边BC、CD相交于点E、F.
用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,如果使三角尺60°角的顶点与点A重合,两边分别与AB、AC重合,将三角尺绕A点按逆时针方向旋转.如图,三角尺的两边分别与菱形的两边BC、CD相交于点E、F. 如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是
如图,在平面直角坐标系中,已知点A(2,0),以OA为边在第一象限内作等边三角形OAB,点P是x轴上一动点 (点P在点A的右侧),以线段BP为边作等边三角形BPQ.设点Q的坐标为(x,y),则y与x之间的关系式是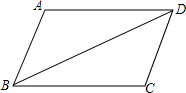 如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.
如图,已知:∠ABC=∠ADC,AD∥BC.请补充完整过程说明:AB=CD的理由.