题目内容
3.计算:(x-2)(x+5)-x(x-2).分析 根据多项式的乘法进行计算解答即可,多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn.
解答 解:原式=x2+5x-2x-10-x2+2x
=5x-10.
点评 此题主要考查多项式乘以多项式的法则.注意不要漏项,漏字母,有同类项的合并同类项.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
13. 二次函数y=ax2-bx的图象如图,若方程ax2-bx+m=0有实数根,则m的最大值为( )
二次函数y=ax2-bx的图象如图,若方程ax2-bx+m=0有实数根,则m的最大值为( )
 二次函数y=ax2-bx的图象如图,若方程ax2-bx+m=0有实数根,则m的最大值为( )
二次函数y=ax2-bx的图象如图,若方程ax2-bx+m=0有实数根,则m的最大值为( )| A. | -3 | B. | 3 | C. | -6 | D. | 0 |
11.一元二次方程x2+2x=0的根是( )
| A. | x=0或x=-2 | B. | x=0或x=2 | C. | x=0 | D. | x=-2 |
8.若不等式组$\left\{\begin{array}{l}{1+x<a}\\{\frac{x+9}{2}≥\frac{x+1}{3}-2}\end{array}\right.$无解,则实数a的取值范围是( )
| A. | a≤-36 | B. | a≥-36 | C. | a<-36 | D. | a>-36 |
15.$\frac{1}{12}$是( )
| A. | 整数 | B. | 有限小数 | C. | 无限循环小数 | D. | 无限不循环小数 |
12.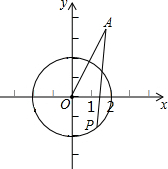 如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
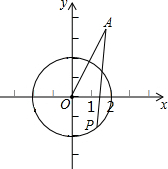 如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
如图,在直角坐标中,⊙0的半径为2,圆心是原点,点A的坐标为(2,2$\sqrt{3}$),P是⊙0上的动点,连接AP,当∠OAP最大时,则点P坐标为(2,0)或(-1,$\sqrt{3}$).
13.已知抛一枚均匀硬币正面朝上的概率为$\frac{1}{2}$,下列说法正确的是( )
| A. | 连续抛一枚均匀硬币2次必有1次正面朝上 | |
| B. | 连续抛一枚均匀硬币10次,不可能正面都朝上 | |
| C. | 大量反复抛一枚均匀硬币,平均每100次出现正面朝上50次 | |
| D. | 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的 |
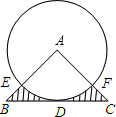 如图,△ABC中,AB=6,AC=8,BC=10,以A为圆心的圆与BC相切于点D,与AB相交于点E,与AC交于点F,则阴影部分的面积S=24-$\frac{144π}{25}$.
如图,△ABC中,AB=6,AC=8,BC=10,以A为圆心的圆与BC相切于点D,与AB相交于点E,与AC交于点F,则阴影部分的面积S=24-$\frac{144π}{25}$. 如图,将一块三角板的直角顶点C放在直线EF上,使得AB∥EF,已知$cosA=\frac{1}{2}$,则sinα=$\frac{1}{2}$.
如图,将一块三角板的直角顶点C放在直线EF上,使得AB∥EF,已知$cosA=\frac{1}{2}$,则sinα=$\frac{1}{2}$.