题目内容
13．已知抛一枚均匀硬币正面朝上的概率为$\frac{1}{2}$，下列说法正确的是（ ）| A． | 连续抛一枚均匀硬币2次必有1次正面朝上 | |
| B． | 连续抛一枚均匀硬币10次，不可能正面都朝上 | |
| C． | 大量反复抛一枚均匀硬币，平均每100次出现正面朝上50次 | |
| D． | 通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的 |
分析 大量反复试验时，某事件发生的频率会稳定在某个常数的附近，这个常数就叫做事件概率的估计值，而不是一种必然的结果，可得答案．
解答 解：A、连续抛一枚均匀硬币2次有可能一次正面朝上，2次正面朝上，0次正面朝上，故A错误；
B、连续抛一枚均匀硬币10次，有可能正面都朝上，故B错误；
C、大量反复抛一枚均匀硬币，平均每100次出现正面朝上的次数不确定，故C错误；
D、通过抛一枚均匀硬币确定谁先发球的比赛规则是公平的，故D正确；
故选：D．
点评 考查利用频率估计概率．大量反复试验下频率稳定值即概率．注意随机事件发生的概率在0和1之间．
练习册系列答案
阅读快车系列答案
相关题目
1．
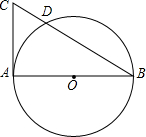如图，AB为⊙O的直径，CA切⊙O于A，CB交⊙O于D，若CD=2，BD=6，求半径r=（ ）
如图，AB为⊙O的直径，CA切⊙O于A，CB交⊙O于D，若CD=2，BD=6，求半径r=（ ）| A． | 2$\sqrt{3}$ | B． | 2$\sqrt{2}$ | C． | 4$\sqrt{3}$ | D． | 4$\sqrt{2}$ |
18．对于反比例函数y=-$\frac{4}{x}$，下列说法正确的是（ ）
| A． | 经过点（2，2） | B． | y随x的增大而增大 | ||
| C． | 两个分支分布在二、四象限 | D． | 图象关于x轴对称 |
