题目内容
6.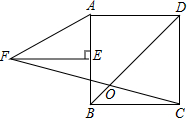 如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )
如图,正方形ABCD中,E为AB中点,FE⊥AB,AF=2AE,FC交BD于O,则∠DOC的度数为( )| A. | 60° | B. | 67.5° | C. | 75° | D. | 54° |
分析 如图,连接DF、BF.如图,连接DF、BF.首先证明∠FDB=$\frac{1}{2}$∠FAB=30°,再证明△FAD≌△FBC,推出∠ADF=∠FCB=15°,由此即可解决问题.
解答 解:如图,连接DF、BF.
∵FE⊥AB,AE=EB,
∴FA=FB,
∵AF=2AE,
∴AF=AB=FB,
∴△AFB是等边三角形,
∵AF=AD=AB,
∴点A是△DBF的外接圆的圆心,
∴∠FDB=$\frac{1}{2}$∠FAB=30°,
∵四边形ABCD是正方形,
∴AD=BC,∠DAB=∠ABC=90°,∠ADB=∠DBC=45°,
∴∠FAD=∠FBC,
∴△FAD≌△FBC,
∴∠ADF=∠FCB=15°,
∴∠DOC=∠OBC+∠OCB=60°.
故选A.
解法二:连接BF.易知∠FCB=15°,∠DOC=∠OBC+∠FCB=45°+15°=60°
点评 本题考查正方形的性质、全等三角形的判定和性质、圆等知识,解题的关键是灵活运用所学知识解决问题,学会添加辅助圆解决问题,属于中考选择题中的压轴题.

练习册系列答案
相关题目
16.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是$\frac{1}{7}$.
1.下列运算结果正确的是( )
| A. | 3a-a=2 | B. | (a-b)2=a2-b2 | C. | 6ab2÷(-2ab)=-3b | D. | a(a+b)=a2+b |
18.下列式子为最简二次根式的是( )
| A. | $\sqrt{\frac{x}{5}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{3{x}^{2}y}$ | D. | $\sqrt{{x}^{2}-9}$ |

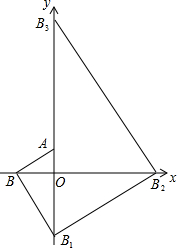 把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009).
把多块大小不同的30°直角三角板如图所示,摆放在平面直角坐标系中,第一块三角板AOB的一条直角边与y轴重合且点A的坐标为(0,1),∠ABO=30°;第二块三角板的斜边BB1与第一块三角板的斜边AB垂直且交y轴于点B1;第三块三角板的斜边B1B2与第二块三角板的斜边BB1垂直且交x轴于点B2;第四块三角板的斜边B2B3与第三块三角板的斜边B1B2垂直且交y轴于点B3;…按此规律继续下去,则点B2017的坐标为(0,-31009). 某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.
某校七年级某班期末测试全班所有学生数学成绩的频数分布直方图如图所示(满分100分),则该班成绩在85.5~95.5这一分数段的学生数是30.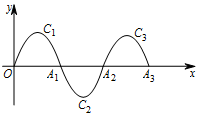 如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )
如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,若点P(2017,m)在第1009段抛物线C1009上,则m的值为( )