题目内容
8.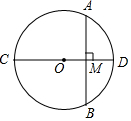 如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )
如图,CD为⊙O的直径,弦AB⊥CD,垂足为M,若AB=12,OM:MD=5:8,则⊙O的周长为( )| A. | 26π | B. | 13π | C. | $\frac{96π}{5}$ | D. | $\frac{39\sqrt{10}π}{5}$ |
分析 连接OA,根据垂径定理得到AM=$\frac{1}{2}$AB=6,设OM=5x,DM=8x,得到OA=OD=13x,根据勾股定理得到OA=$\frac{1}{2}$×13,于是得到结论.
解答  解:连接OA,
解:连接OA,
∵CD为⊙O的直径,弦AB⊥CD,
∴AM=$\frac{1}{2}$AB=6,
∵OM:MD=5:8,
∴设OM=5x,DM=8x,
∴OA=OD=13x,
∴AM=12x=6,
∴x=$\frac{1}{2}$,
∴OA=$\frac{1}{2}$×13,
∴⊙O的周长=2OA•π=13π,
故选B.
点评 本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.

练习册系列答案
相关题目
16.如果任意选择一对有序整数(m,n),其中|m|≤1,|n|≤3,每一对这样的有序整数被选择的可能性是相等的,那么关于x的方程x2+nx+m=0有两个相等实数根的概率是$\frac{1}{7}$.
3. 已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )
 已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
已知,如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变;
那么,你认为( )
| A. | 甲、乙都对 | B. | 乙对甲不对 | C. | 甲对乙不对 | D. | 甲、乙都不对 |
13.2016年安徽省参加中考的学生数为56.3万人,其中“56.3万”用科学记数法表示为( )
| A. | 5.63×104 | B. | 5.63×105 | C. | 56.3×104 | D. | 0.563×106 |
20.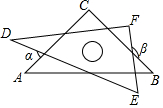 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
 小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )
小明把一副含45°,30°的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D=30°,则∠α+∠β等于( )| A. | 180° | B. | 210° | C. | 360° | D. | 270° |
18.下列式子为最简二次根式的是( )
| A. | $\sqrt{\frac{x}{5}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{3{x}^{2}y}$ | D. | $\sqrt{{x}^{2}-9}$ |
