题目内容
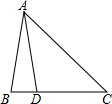 如图,在△ABC中,AB=AD=DC,AC=BC,则∠C=
如图,在△ABC中,AB=AD=DC,AC=BC,则∠C=考点:等腰三角形的性质
专题:
分析:设∠C=x°,根据等腰三角形的性质及三角形外角的性质得出∠DAC=∠C=x°,∠ADB=∠DAC+∠C=2x°,∠B=∠ADB=2x°,∠B=∠CAB=2x°,于是∠BAD=∠CAB-∠DAC=x°.然后在△ABD中,根据三角形内角和定理得出x+2x+2x=180,解方程即可.
解答:解:设∠C=x°.
∵AD=DC,
∴∠DAC=∠C=x°,
∴∠ADB=∠DAC+∠C=2x°.
∵AB=AD,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠B=∠CAB=2x°,
∴∠BAD=∠CAB-∠DAC=2x°-x°=x°.
在△ABD中,∵∠BAD+∠B+∠ADB=180°,
∴x+2x+2x=180,
∴x=36,
∴∠C=36°.
故答案为:36.
∵AD=DC,
∴∠DAC=∠C=x°,
∴∠ADB=∠DAC+∠C=2x°.
∵AB=AD,
∴∠B=∠ADB=2x°,
∵AC=BC,
∴∠B=∠CAB=2x°,
∴∠BAD=∠CAB-∠DAC=2x°-x°=x°.
在△ABD中,∵∠BAD+∠B+∠ADB=180°,
∴x+2x+2x=180,
∴x=36,
∴∠C=36°.
故答案为:36.
点评:本题考查了等腰三角形的性质,三角形内角和定理及三角形外角的性质等知识.此类已知三角形边之间的关系求角的度数的题,一般是利用等腰三角形的性质、三角形外角的性质得出有关角的度数,进而根据三角形内角和定理列出方程求出所求角的度数.

练习册系列答案
相关题目
下列分解因式正确的是( )
| A、-x2-y2=-(x+y)(x-y) |
| B、x2y+2xy+4y=y(x+2)2 |
| C、49x2-x2y2=(xy+7x)(xy-7x) |
| D、16x2+4y2-16xy=4(2x-y)2 |
 如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm.
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm. 如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.
如图,⊙O为Rt△ABC的内切圆,∠ACB=90°,若∠BOC=105°,AB=12cm,求BC的长.