题目内容
 如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm.
如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是3cm.(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
考点:切线的判定,扇形面积的计算
专题:
分析:(1)连接OD,由∠AOD=2∠ACD=90°,结合AB∥DE,可得∠ODE=90°,可知DE为⊙O的切线;
(2)由条件可先求得梯形OBED的面积再减去扇形BOD的面积即可.
(2)由条件可先求得梯形OBED的面积再减去扇形BOD的面积即可.
解答: 解:(1)DE与⊙O相切,理由如下:
解:(1)DE与⊙O相切,理由如下:
如图,连接OD,
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵DE∥AB,
∴∠ODE=∠AOD=90°,
∴OD⊥DE,
∴DE与⊙O相切;
(2)∵AB∥DE,AD∥BE,
∴四边形ABED是平行四边形,
∴AB=DE=6cm,且OB=OD=3cm,
∴S梯形OBED=
(OB+DE)•OD=
×(3+6)×3=
(cm2),S扇形OBD=
=
×π×32=
(cm2),
∴S阴影=S梯形OBED-S扇形OBD=(
-
)(cm2).
 解:(1)DE与⊙O相切,理由如下:
解:(1)DE与⊙O相切,理由如下:如图,连接OD,
∵∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∵DE∥AB,
∴∠ODE=∠AOD=90°,
∴OD⊥DE,
∴DE与⊙O相切;
(2)∵AB∥DE,AD∥BE,
∴四边形ABED是平行四边形,
∴AB=DE=6cm,且OB=OD=3cm,
∴S梯形OBED=
| 1 |
| 2 |
| 1 |
| 2 |
| 27 |
| 2 |
| 90π•OB2 |
| 360 |
| 1 |
| 4 |
| 9π |
| 4 |
∴S阴影=S梯形OBED-S扇形OBD=(
| 27 |
| 2 |
| 9π |
| 4 |
点评:本题主要考查切线的判定及扇形面积的计算,掌握切线的两种判定方法及扇形的面积公式是解题的关键.

练习册系列答案
相关题目
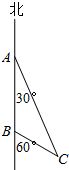 如图,一条船从海岛A处向正南航行到达海岛B处,从海岛A处测得灯塔C在南偏东30°方向,从海岛B处测得灯塔C在南偏东60°方向,已知A、B两海岛距离25海里,则海岛B到灯塔C的距离为
如图,一条船从海岛A处向正南航行到达海岛B处,从海岛A处测得灯塔C在南偏东30°方向,从海岛B处测得灯塔C在南偏东60°方向,已知A、B两海岛距离25海里,则海岛B到灯塔C的距离为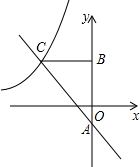 如图,一次函数y=kx-1(k≠0)的图象与反比例函数y=
如图,一次函数y=kx-1(k≠0)的图象与反比例函数y=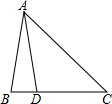 如图,在△ABC中,AB=AD=DC,AC=BC,则∠C=
如图,在△ABC中,AB=AD=DC,AC=BC,则∠C= 晶晶在木板上钉了五个钉子A、B、C、D、E,其中A、B、C、D四个钉子在同一条直线上.
晶晶在木板上钉了五个钉子A、B、C、D、E,其中A、B、C、D四个钉子在同一条直线上.