题目内容
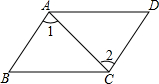如图，AB∥CD，AB=CD．问：△ABC和△CDA是全等三角形吗？为什么？考点：全等三角形的判定
专题：常规题型
分析：先根据平行线的性质得∠1=∠2，然后根据“SAS”可判断△ABC≌△CDA．
解答：解：△ABC和△CDA全等．理由如下：
∵AB∥CD，
∴∠1=∠2，
在△ABC和△CDA中，
，
∴△ABC≌△CDA．
∵AB∥CD，
∴∠1=∠2，
在△ABC和△CDA中，
|
∴△ABC≌△CDA．
点评：本题考查了三角形全等的判定：一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．
练习册系列答案
习题精选系列答案
相关题目
王先生有块地如图所示，已知∠ABC=90°，AB=3米，BC=4米，CD=12米，AD=13米，求这块地的面积多大？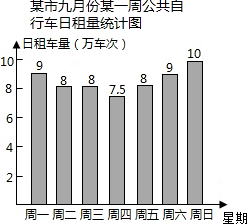
作为某市政府民生实事之一的公共自行车建设工作已基本完成，某部门对2014年九月份中的7天进行了公共自行车日租车量的统计，结果如图：既不是中心对称图形又不是轴对称图形的是（ ）
| A、平行四边形 | B、等腰三角形 |
| C、直角梯形 | D、等腰梯形 |
如图，△ABC中，∠B的平分线与∠C的外角的平分线交于P点，PD⊥AC于D，PH⊥BA于H，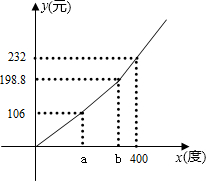
自2012年6月1日起，全国实施了阶梯电价．某省出台了阶梯电价方案：电价分“三档”收费，第一档为a度，居民用电量低于a度的部分，执行现行的标准电价（0.53元/度）；第二档为a～b度，居民月用电量在a～b之间的部分，电价在一档电价的基础上提高0.05元/度；第三档为超过b度，居民月用电量高于b度的部分，电价在一档电价的基础上提高m元/度．实施阶梯电价后，月电费y（元）与月用电量x（度）之间的函数关系如图所示．