题目内容
16．求不等式3（x+1）≥5x-3的正整数解．分析 首先利用不等式的基本性质解不等式，再从不等式的解集中找出适合条件的正整数即可．
解答 解：3（x+1）≥5x-3，
去括号得，3x+3≥5x-3，
移项湖北得，-2x≥-6，
系数化为1得，x≤3，
故不等式3（x+1）≥5x-3的正整数解为1，2，3．
点评 本题考查了一元一次不等式的整数解，正确解不等式，求出解集是解答本题的关键．解不等式应根据不等式的基本性质．
练习册系列答案
相关题目
7．下列等式从左到右的变形，属于因式分解的是（ ）
| A． | x3-x=x（x+1）（x-1） | B． | x2+2x+1=x（x+2）+1 | C． | （x+1）（x+3）=x2+4x+3 | D． | a（x-y）=ax-ay |
4．
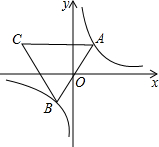已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点，连接AO并延长交另一分支于点B，以AB为一边作等边三角形ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为（ ）
已知点A是双曲线y=$\frac{2}{x}$在第一象限上的动点，连接AO并延长交另一分支于点B，以AB为一边作等边三角形ABC，点C在第二象限，随着点A的运动，点C的位置也不断的变化，但始终在一函数图象上运动，则这个函数的解析式为（ ）| A． | y=-$\frac{2}{x}$（x＜0） | B． | y=-$\frac{4}{x}$（x＜0） | C． | y=-$\frac{6}{x}$（x＜0） | D． | y=-$\frac{8}{x}$（x＜0） |
11．在一个直径为6cm的圆中，小明画了一个圆心角为120°的扇形，则这个扇形的面积为（ ）
| A． | πcm2 | B． | 2πcm2 | C． | 3πcm2 | D． | 6πcm2 |
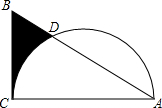如图，在Rt△ABC中，∠C=90°，∠A=30°，AB=4，以AC为直径作半圆交AB于点D，则图中阴影部分的面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$．