题目内容
5.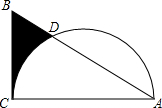 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC为直径作半圆交AB于点D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=4,以AC为直径作半圆交AB于点D,则图中阴影部分的面积为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
分析 由∠A的度数求出∠ADO度数,利用30°直角三角形的性质求出BC的长,利用勾股定理求出AC的长,阴影部分面积=直角三角形ABC面积-扇形OCD面积-三角形AOD面积,求出即可.
解答 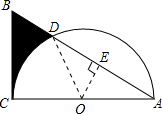 解:连接半圆圆心O与D,过点O作OE⊥AB,
解:连接半圆圆心O与D,过点O作OE⊥AB,
在Rt△ABC中,∠A=30°,AB=4,
∴BC=$\frac{1}{2}$AB=2,∠COD=60°,
根据勾股定理得:AC=2$\sqrt{3}$,
∴OA=$\sqrt{3}$,
∴OE=$\frac{\sqrt{3}}{2}$,AE=$\frac{3}{2}$,
∴AD=3,
则S阴影=S△ABC-S扇形COD-S△AOD=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π•(\sqrt{3})^{2}}{360}$-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$=$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$,
故答案为$\frac{5\sqrt{3}}{4}$-$\frac{π}{2}$.
点评 本题考查了切线的判定,以及扇形面积的计算,涉及的知识有:等腰三角形的性质,含30°直角三角形的性质,以及勾股定理,熟练掌握扇形面积公式S=$\frac{nπ{r}^{2}}{360}$是解本题的关键.

练习册系列答案
相关题目
14.某公司近经过市场调研,决定下月对甲、乙两种产品进行“限产压库”,公司决定这两种产品下月共生产20件,这20件产品的产值y不少于1140万元,不多于1200万元.已知有关数据如表:
(1)若生产甲产品x(x为正整数)件,写出x满足的不等式组;
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
| 产品 | 每件产品的产量 | 每件产品用工时数 |
| 甲 | 45万元 | 150 |
| 乙 | 75万元 | 190 |
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
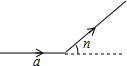 小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.
小明同学在社团活动中给发明的机器人设置程序:(a,n).机器人执行步骤是:向正前方走am后向左转n°,再依次执行相同程序,直至回到原点.现输入a=6,n=40,那么机器人回到原点共走了54m.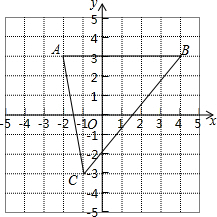 如图,已知A(-2,3)、B(4,3)、C(-1,-3)
如图,已知A(-2,3)、B(4,3)、C(-1,-3)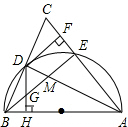 如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )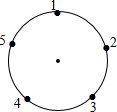 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数2对应的点上.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数2对应的点上.