题目内容
6.设抛物线y=-x2+2x+3的顶点为E,与y轴交于点C,EF⊥x轴于点,若点M(m,0)是x轴上的动点,且满足以MC为直径的圆与线段EF有公共点,则实数m的取值范围是-$\frac{5}{4}$≤m≤5.分析 根据题意表示出圆心的坐标、圆的半径、圆心到EF的距离,列出不等式求出答案.
解答  解:∵M(m,0),C(0,3),
解:∵M(m,0),C(0,3),
∴圆心N的坐标($\frac{m}{2}$,$\frac{3}{2}$),
圆N的半径为:$\frac{\sqrt{{m}^{2}+9}}{2}$,
圆心到EF的距离为:|1-$\frac{m}{2}$|,
由题意得,
|1-$\frac{m}{2}$|≤$\frac{\sqrt{{m}^{2}+9}}{2}$≤$\sqrt{(\frac{m}{2}-1)^{2}+(4-\frac{3}{2})^{2}}$,
解得:-$\frac{5}{4}$≤m≤5.
故答案为:-$\frac{5}{4}$≤m≤5.
点评 本题考查的是直线与圆的关系和二次函数的性质,掌握若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离是解题的关键.

练习册系列答案
相关题目
14.某公司近经过市场调研,决定下月对甲、乙两种产品进行“限产压库”,公司决定这两种产品下月共生产20件,这20件产品的产值y不少于1140万元,不多于1200万元.已知有关数据如表:
(1)若生产甲产品x(x为正整数)件,写出x满足的不等式组;
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
| 产品 | 每件产品的产量 | 每件产品用工时数 |
| 甲 | 45万元 | 150 |
| 乙 | 75万元 | 190 |
(2)请你帮助公司设计出所有符合题意的生产方案;
(3)若从节省工时数考虑,通过计算,你认为哪种方案最好?
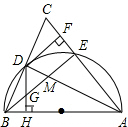 如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )
如图,在△ABC中,AB=AC,以AB为直径的半圆O交BC于点D,交AC于点E,连接AD、BE交于点M,过点D作DH⊥AB于点H,交BE于点G,有下列结论:①BD=CD;②DF是⊙O的切线;③∠DAC=∠BDH;④BM=2DG.其中,成立的个数为( )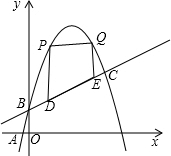 如图,已知一次函数y=$\frac{1}{2}$x+m与二次函数y=-x2+ax+b的图象相交于点B(0,1)和点C.且抛物线与x轴的一个交点是A(2-$\sqrt{5}$,0).
如图,已知一次函数y=$\frac{1}{2}$x+m与二次函数y=-x2+ax+b的图象相交于点B(0,1)和点C.且抛物线与x轴的一个交点是A(2-$\sqrt{5}$,0).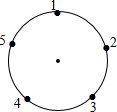 如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数2对应的点上.
如图,一只青蛙在圆周上标有数字的五个点上跳,若它停在奇数点上,则下一次沿顺时针方向跳两个点;若停在偶数点上,则下一次沿逆时针方向跳一个点,若青蛙从4这点开始跳,则经2015次跳后它停在数2对应的点上. 小红家九月份的生活用水情况如图所示,小红的妈妈说:“洗衣用水约为2.6立方米.”请你估计小红家一年的总用水量?
小红家九月份的生活用水情况如图所示,小红的妈妈说:“洗衣用水约为2.6立方米.”请你估计小红家一年的总用水量?