题目内容
15.(1)解方程组:$\left\{\begin{array}{l}{x+y=0}\\{2x+3y=3}\end{array}\right.$;(2)解不等式组$\left\{\begin{array}{l}{3x-2≤x}\\{\frac{2x+1}{5}<\frac{x+1}{2}}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)加减消元法求解可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
解答 解:(1)$\left\{\begin{array}{l}{x+y=0}&{①}\\{2x+3y=3}&{②}\end{array}\right.$,
①×3-②,得:x=-3,
将x=-3代入x+y=0,得:y=3,
则方程组的解为$\left\{\begin{array}{l}{x=-3}\\{y=3}\end{array}\right.$;
(2)解不等式3x-2≤x,得:x≤1,
解不等式$\frac{2x+1}{5}$$<\frac{x+1}{2}$,得:x>-3,
则不等式组的解集为-3<x≤1,
将解集表示在数轴上如下:
点评 本题考查的是解二元一次方程组和一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
13. 如图,在△ABC中,∠ABC=50°,AD,CD分别平分∠BAC,∠ACB,则∠ADC等于( )
如图,在△ABC中,∠ABC=50°,AD,CD分别平分∠BAC,∠ACB,则∠ADC等于( )
 如图,在△ABC中,∠ABC=50°,AD,CD分别平分∠BAC,∠ACB,则∠ADC等于( )
如图,在△ABC中,∠ABC=50°,AD,CD分别平分∠BAC,∠ACB,则∠ADC等于( )| A. | 125° | B. | 105° | C. | 115° | D. | 100° |
10.下列分式中,属于最简分式的是( )
| A. | $\frac{4}{2x}$ | B. | $\frac{{x}^{2}-1}{{x}^{2}+1}$ | C. | $\frac{{x}^{2}-36}{2x+12}$ | D. | $\frac{1-x}{x-1}$ |
20.已知?ABCD的周长为32,AB=6,则BC等于( )
| A. | 10 | B. | 12 | C. | 24 | D. | 28 |
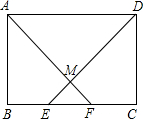 如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:
如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证: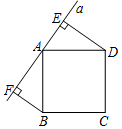 如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为14.
如图,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,AB=10,则EF的长为14.