题目内容
3.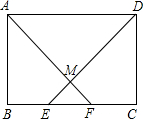 如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:
如图,在矩形ABCD中,点E.点F在BC边上,且BE=CF,AF,DE交于点M.求证:①△ABF≌△DCE
②AM=DM.
分析 ①根据矩形的性质可求得AB=DC,∠B=∠C,结合条件可求得BF=CE,则可证得结论;
②由全等三角形的性质可求得∠AFB=∠DEC,再结合AD∥BC,则可求得∠MDA=∠MAD,可求得MA=MD.
解答 证明:
①∵四边形ABCD为矩形,
∴AB=DC,∠B=∠C,
∵BE=CF,
∴BE+EF=EF+CF,即BF=CE,
在△ABF和△DCE中
$\left\{\begin{array}{l}{AB=CD}\\{∠B=∠C}\\{BF=CE}\end{array}\right.$
∴△ABF≌△DCE(SAS);
②∵△ABF≌△DCE,
∴∠AFB=∠DEC,
∵AD∥BC,
∴∠AFB=∠MAD,∠DEC=∠MDA,
∴∠MAD=∠MDA,
∴MA=MD.
点评 本题主要考查矩形的性质,掌握矩形的对边平行且相等、每个角都是直角是解题的关键.

练习册系列答案
相关题目
2.下列运算中,结果错误的是( )
| A. | 4a-a=3a | B. | a10÷a2=a8 | C. | a2+a3=a5 | D. | a3•a4=a7 |
20.下列几何体中,主视图为三角形的是( )
| A. |  | B. |  | C. |  | D. |  |
12. 将如图所示的图案平移后得到的图案是( )
将如图所示的图案平移后得到的图案是( )
 将如图所示的图案平移后得到的图案是( )
将如图所示的图案平移后得到的图案是( )| A. |  | B. |  | C. |  | D. |  |
13. 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
 如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为( )| A. | $\frac{1}{2}$π | B. | $\frac{3}{4}$π | C. | $\frac{3}{8}$π | D. | π |

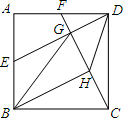 如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.
如图,在正方形ABCD中,点E是AB中点,点F是AD上一点,且DE=CF,ED、FC交于点G,连接BG,BH平分∠GBC交FC于H,连接DH.