题目内容
 如图,点P是函数y=
如图,点P是函数y=| 2 |
| x |
(1)若△PAB是直角三角形,请直接写出点P的坐标
(2)连结PA、PB、AB,设△PAB的面积为S,点P的横坐标为t.请写出S关于t的函数关系式,并指出自变量t的取值范围;
(3)阅读下面的材料回答问题
阅读材料:当a>0时,a+
| 1 |
| a |
| a |
| 1 | ||
|
| a |
| 1 | ||
|
因为(
| a |
| 1 | ||
|
| a |
| 1 | ||
|
所以a=1时,a+
| 1 |
| a |
根据上述材料在(2)中研究当t为何值时△PAB的面积S有最小值,并求出S的最小值.
考点:反比例函数综合题
专题:
分析:(1)当∠PAB=90°时,利用△OAB为等腰直角三角形得到∠OAB=45°,则PA与y轴的夹角为45°,此时P点的纵坐标比横坐标大1,设P(a,a+1),然后利用a(a+1)=2求出a=1得到P点坐标为(1,2);同理可得当∠PBA=90°时,P点坐标为(2,1);由于直线y=x与反比例函数的交点坐标为(
,
),所以反比例函数图象上到原点的最近距离为2,而AB=
,则以AB为直径的圆与反比例函数图象没有公共点,所以∠APB不等为直角;
(2)连结OP,AB,根据反比例函数图象上点的坐标特征可设P点坐标为(t,
),利用三角形面积公式和S=S△PAO+S△POB-S△OAB求解;
(3)由于S═
+
-
,根据阅读材料得到当t>0时,
+
=(
-
)2+
,利用非负数的性质得当t=
时,
+
有最小值为
,所以t=
时,S有最小值为
-
.
| 2 |
| 2 |
| 2 |
(2)连结OP,AB,根据反比例函数图象上点的坐标特征可设P点坐标为(t,
| 2 |
| t |
(3)由于S═
| t |
| 2 |
| 1 |
| t |
| 1 |
| 2 |
| t |
| 2 |
| 1 |
| t |
|
|
| 2 |
| 2 |
| t |
| 2 |
| 1 |
| t |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
解答:解: (1)当P点坐标为(2,1)或(1,2)时,△PAB是直角三角形;
(1)当P点坐标为(2,1)或(1,2)时,△PAB是直角三角形;
故答案为(2,1)或(1,2);
(2)连结OP,AB,如图,设P点坐标为(t,
),
S=S△PAO+S△POB-S△OAB
=
×1×t+
×1×
-
×1×1
=
+
-
=
(t>0);
(3)当t>0时,
+
=(
)2-
+(
)2+
=(
-
)2+
,
因为(
-
)2≥0,当
=
,即t=
时,(
-
)2=0,
所以当t=
时,
+
有最小值为
,
所以t=
时,S有最小值为
-
.
 (1)当P点坐标为(2,1)或(1,2)时,△PAB是直角三角形;
(1)当P点坐标为(2,1)或(1,2)时,△PAB是直角三角形;故答案为(2,1)或(1,2);
(2)连结OP,AB,如图,设P点坐标为(t,
| 2 |
| t |
S=S△PAO+S△POB-S△OAB
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| t |
| 1 |
| 2 |
=
| t |
| 2 |
| 1 |
| t |
| 1 |
| 2 |
=
| t2-t+2 |
| 2t |
(3)当t>0时,
| t |
| 2 |
| 1 |
| t |
|
| 2 |
|
| 2 |
|
|
| 2 |
因为(
|
|
| t |
| 2 |
| 1 |
| t |
| 2 |
|
|
所以当t=
| 2 |
| t |
| 2 |
| 1 |
| t |
| 2 |
所以t=
| 2 |
| 2 |
| 1 |
| 2 |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、等腰直角三角形的性质;理解坐标与图形的性质;会利用非负数的性质解决最值问题.

练习册系列答案
相关题目
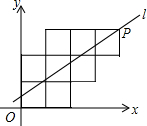 八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
 在平面直角坐标系中xOy中,点A与原点O重合,点B(4,0),点E、(0,2),过点E作平行于x轴的直线l,点C、D在直线上运动(点C在点D的左侧),CD=4,连接BC,过点A作关于直线BC的对称点A′,连接AC、A′C.
在平面直角坐标系中xOy中,点A与原点O重合,点B(4,0),点E、(0,2),过点E作平行于x轴的直线l,点C、D在直线上运动(点C在点D的左侧),CD=4,连接BC,过点A作关于直线BC的对称点A′,连接AC、A′C. 请填空完成下面的证明:
请填空完成下面的证明: 如图,BD是平行四边形?ABCD的对角线,E、F在BD上.
如图,BD是平行四边形?ABCD的对角线,E、F在BD上.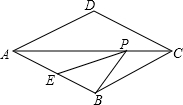 如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是
如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,当P移动到AC的中点时,则PE+PB的值是