题目内容
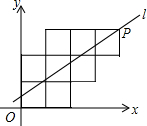 八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )
八个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
考点:一次函数综合题
专题:
分析:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,易知OB=3,利用三角形的面积公式和已知条件求出点A的坐标,根据待定系数法即可得到该直线l的解析式.
解答: 解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,
解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8÷2+1=5,
∴
BP•AB=5,
∴AB=2.5,
∴OA=3-2.5=0.5,
由此可知直线l经过(0,0.5),(4,3)
设直线方程为y=kx+b,则
,
解得
.
∴直线l解析式为y=
x+
.
故选:A.
 解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,
解:直线l和八个正方形的最上面交点为P,过P作PB⊥OB于B,过P作PC⊥OC于C,∵正方形的边长为1,
∴OB=3,
∵经过P点的一条直线l将这八个正方形分成面积相等的两部分,
∴三角形ABP面积是8÷2+1=5,
∴
| 1 |
| 2 |
∴AB=2.5,
∴OA=3-2.5=0.5,
由此可知直线l经过(0,0.5),(4,3)
设直线方程为y=kx+b,则
|
解得
|
∴直线l解析式为y=
| 5 |
| 8 |
| 1 |
| 2 |
故选:A.
点评:此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质,此题难度较大,解题的关键是作PB⊥y轴,作PC⊥x轴,根据题意即得到:直角三角形ABP面积是5,利用三角形的面积公式求出AB的长.

练习册系列答案
相关题目
为了了解一片实验田的某种水稻的穗长情况,从中抽取了400个稻穗测量长度,结果有40个稻穗测量长度超过超过30cm,在这个问题中,下列说法正确的是( )
| A、400个稻穗的穗长情况是总体 |
| B、40个稻穗的穗长情况是样本 |
| C、每个稻穗的穗长情况是个体 |
| D、样本容量是40 |
 如图,直线a∥b,∠1=115°,∠2=105°,则∠3的度数为( )
如图,直线a∥b,∠1=115°,∠2=105°,则∠3的度数为( )| A、120° | B、130° |
| C、140° | D、80° |
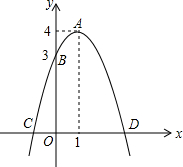 如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点,点P是x轴上的一个动点.
如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C、D两点,点P是x轴上的一个动点. 如图,点P是函数y=
如图,点P是函数y=