题目内容
6. 如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为(0,-$\frac{9}{4}$).
如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为(0,-$\frac{9}{4}$).
分析 由折叠的性质可知,∠B′AC=∠BAC,∠BAC=∠DCA,易得DC=DA,设OD=x,则DC=6-x,在Rt△AOD中,由勾股定理得OD,得OD的坐标.
解答 解:由折叠的性质可知,∠B′AC=∠BAC,
∵四边形OABC为矩形,
∴OC∥AB,
∴∠BAC=∠DCA,
∴∠B′AC=∠DCA,
∴AD=CD,
设OD=x,则DC=6-x,在Rt△AOD中,由勾股定理得,
OA2+OD2=AD2,
即9+x2=(6-x)2,
解得:x=$\frac{9}{4}$,
∴点D的坐标为:(0,$-\frac{9}{4}$),
故答案为:(0,-$\frac{9}{4}$).
点评 本题主要考查了翻折变换的性质及其应用问题,灵活运用有关定理来分析、判断、推理或解答是解题的关键.

练习册系列答案
相关题目
17.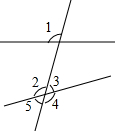 如图,下列各组角中,是对顶角的一组是( )
如图,下列各组角中,是对顶角的一组是( )
 如图,下列各组角中,是对顶角的一组是( )
如图,下列各组角中,是对顶角的一组是( )| A. | ∠1和∠2 | B. | ∠3和∠5 | C. | ∠3和∠4 | D. | ∠1和∠5 |
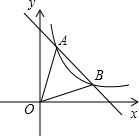 如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点,
如图,一次函数y=k1x+b的图象与反比例函数y=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点,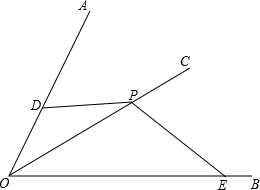 如图,OC平分∠AOB,∠DOE+∠DPE=180°.求证:PD=PE.
如图,OC平分∠AOB,∠DOE+∠DPE=180°.求证:PD=PE.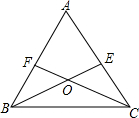 已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.
已知:∠A=60°,BE平分∠ABC,CF平分∠ACB,BE交CF于O,求证:OE=OF.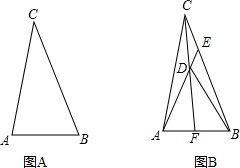 如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.