题目内容
17.已知函数y=(m-2)x${\;}^{{m}^{2}-5}$是反比例函数.(1)求m的值;
(2)画出函数的图象.
分析 (1)根据反比例函数的定义确定m的值即可;
(2)利用描点法作出函数的图象即可;
解答 解:(1)∵函数y=(m-2)x${\;}^{{m}^{2}-5}$是反比例函数,
∴$\left\{\begin{array}{l}{{m}^{2}-5=-1}\\{m-2≠0}\end{array}\right.$,
∴m=-2;
(2)当m=-2时反比例函数的解析式为y=-$\frac{4}{x}$,
图象为:
点评 本题考查了反比例函数的图象级反比例函数的定义,解题的关键是能够利用反比例函数的定义确定反比例函数的解析式,难度不大.

练习册系列答案
相关题目
5.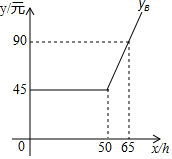 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:
设每月上网学习时间为x(h)小时,方案A,B的收费金额分别为yA (元)、yB(元).
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
 某网站策划了A、B两种上网的月收费方式:
某网站策划了A、B两种上网的月收费方式:| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | m | n | P |
如图是yB与x之间函数关系的图象
(友情提示:若累计上网时间不超出“包时上网时间”,则只收”月使用费“;若累计上网时间不超出“包时上网时间”,则对超出部分再加收”超时费“)
(1)m=45;n=50p=0.05.
(2)写出yA与x之间的函数关系式.
(3)若每月上网的时间为29小时,请说明选取哪种方式能节省上网费?
6.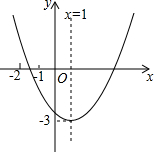 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
①2a-b=0;
②9a+3b+c<0;
③关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
④8a+c<0.
其中正确的个数是( )
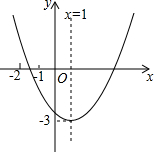 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:①2a-b=0;
②9a+3b+c<0;
③关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
④8a+c<0.
其中正确的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
7.下列图形:平行四边形、矩形、菱形、圆、等腰三角形,这些图形中只是轴对称图形的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
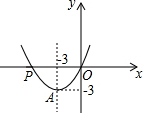 已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
已知抛物线y=ax2+bx经过点A(-3,-3)和点P(m,0),且m≠0.
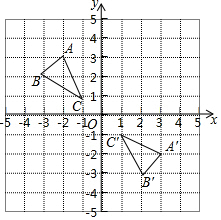 如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)
如图,在平面直角坐标系中,△ABC的顶点坐标为A(-2,3)、B(-3,2)、C(-1,1)