题目内容
在平面直角坐标系中A(2,-3),B(4,-1),若C(a+3,0),D(a,0),则当a= 时四边形ABCD周长最短.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B′(5,3),连接BB′,与x轴交于点C,易得四边形A′B′DC为平行四边形,得到DA′=CB′=DA,则AD+BC=BB′,根据两点之间线段最短得到此时AD+CD最小,即四边形ABCD的周长最短.然后用待定系数法求出直线BB′的解析式y=4x-17,把C(a+3,0)代入解析式即可求得a的值.
解答: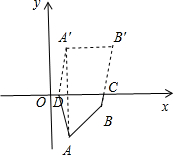 解:作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B′(5,3),连接BB′,与x轴交于点C,过A′作A′D∥BB′交x轴于D,如图,
解:作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B′(5,3),连接BB′,与x轴交于点C,过A′作A′D∥BB′交x轴于D,如图,
∴DA′=DA,
∵A′B′∥CD,
∴四边形A′B′DC为平行四边形,
∴DA′=CB′,
∴DA=CB′,
∴AD+BC=BB′,此时AC+BD最小,
而CD与AB的长一定,
∴此时四边形ABDC的周长最短.
设直线BB′的解析式为y=kx+b,
把B(4,-1)、B′(5,3)分别代入得
,
解得k=4,b=-17,
∴直线BB′的解析式为y=4x-17,
∵C(a+3,0),
∴4(a+3)-17=0,
解得a=
,
故答案为
.
 解:作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B′(5,3),连接BB′,与x轴交于点C,过A′作A′D∥BB′交x轴于D,如图,
解:作点A关于x轴的对称点A′,则A′的坐标为(2,3),把A′向右平移3个单位得到点B′(5,3),连接BB′,与x轴交于点C,过A′作A′D∥BB′交x轴于D,如图,∴DA′=DA,
∵A′B′∥CD,
∴四边形A′B′DC为平行四边形,
∴DA′=CB′,
∴DA=CB′,
∴AD+BC=BB′,此时AC+BD最小,
而CD与AB的长一定,
∴此时四边形ABDC的周长最短.
设直线BB′的解析式为y=kx+b,
把B(4,-1)、B′(5,3)分别代入得
|
解得k=4,b=-17,
∴直线BB′的解析式为y=4x-17,
∵C(a+3,0),
∴4(a+3)-17=0,
解得a=
| 5 |
| 4 |
故答案为
| 5 |
| 4 |
点评:本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.也考查了坐标变换以及待定系数法求一次函数的解析式.

练习册系列答案
相关题目
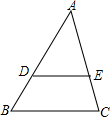 如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )
如图,在△ABC中,DE∥BC,DE分别与AB、AC相交于点D、E,若AD=4,AB=6,则DE:BC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
从正面看、从左面看、从上面看都一样的几何体是( )
| A、圆柱 | B、长方体 | C、球 | D、五棱柱 |
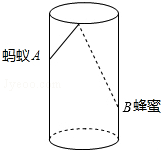 如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为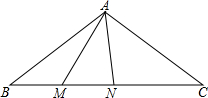 如图,ABC中,AB=AC,BC=16,cosB=
如图,ABC中,AB=AC,BC=16,cosB=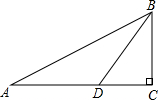 如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC=
如图,在直角△ABC中,∠C=90°,点D在线段AC上,且∠A=30°,∠BDC=60°,AD=2,则BC= 已知AO⊥BO,DO⊥CO,∠AOD=4∠BOC,则∠AOD的度数为
已知AO⊥BO,DO⊥CO,∠AOD=4∠BOC,则∠AOD的度数为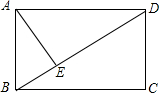 如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.
如图,在矩形ABCD中,AE⊥BD,垂足为E,BE=2,ED=6,求矩形ABCD的周长.