题目内容
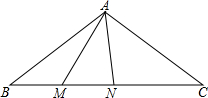 如图,ABC中,AB=AC,BC=16,cosB=
如图,ABC中,AB=AC,BC=16,cosB=| 4 |
| 5 |
考点:相似三角形的判定与性质
专题:
分析:如图,作辅助线;求出AB=10;证明△ABN∽△MCA,得到
=
,故BN•CM=AB•AC=100.
| AB |
| MC |
| BN |
| AC |
解答: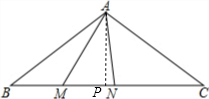 解:如图,过点A作AP⊥BC于点P.
解:如图,过点A作AP⊥BC于点P.
∵AB=AC,BC=16,
∴BP=PC=8,∠B=∠C;而cosB=
,
∴
=
,AB=10;
∵∠MAN=∠C,
∴∠MAN+∠NAC=∠NAC+∠C;
∵∠MAC=∠MAN+∠NAC,∠ANB=∠NAC+∠C,
∴∠MAC=∠ANB,而∠B=∠C,
∴△ABN∽△MCA,
∴
=
,
∴BN•CM=AB•AC=100.
故答案为100.
 解:如图,过点A作AP⊥BC于点P.
解:如图,过点A作AP⊥BC于点P.∵AB=AC,BC=16,
∴BP=PC=8,∠B=∠C;而cosB=
| 4 |
| 5 |
∴
| BP |
| AB |
| 4 |
| 5 |
∵∠MAN=∠C,
∴∠MAN+∠NAC=∠NAC+∠C;
∵∠MAC=∠MAN+∠NAC,∠ANB=∠NAC+∠C,
∴∠MAC=∠ANB,而∠B=∠C,
∴△ABN∽△MCA,
∴
| AB |
| MC |
| BN |
| AC |
∴BN•CM=AB•AC=100.
故答案为100.
点评:该题主要考查了相似三角形的判定及其性质、等腰三角形的性质等知识点及其应用问题;牢固掌握相似三角形的判定及其性质、等腰三角形的性质是解题的基础和关键.

练习册系列答案
相关题目
 已知a、b、c在数轴上的位置如图所示,化简|b-a|+|2a+c|-|c-b|的结果是( )
已知a、b、c在数轴上的位置如图所示,化简|b-a|+|2a+c|-|c-b|的结果是( )| A、-a-2c | B、3a |
| C、a | D、3a-2b |
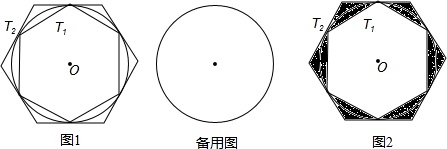
 如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )
如图,是某个几何体从不同方向看到的形状图(视图),这个几何体的表面能展开成下面的哪个平面图形?( )



 如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.
如图,AB是半圆的直径,AC为弦,OD⊥AB,交AC于点D,垂足为O,⊙O的半径为4,OD=3,求CD的长.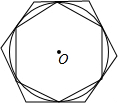 如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形)
如图,正六边形T1的6个顶点都在⊙O上,正六边形T2的6条边都和⊙O相切(我们称T1、T2分别为⊙O的内接正六边形和外切正六边形) 如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.
如图,已知⊙O中,弦AB的长等于⊙O的半径,求弦所对的圆心角和圆周角的度数.