题目内容
12.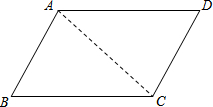 我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.
我们规定,两组对边分别平行的四边形叫做平行四边形.如图,四边形ABCD,小明同学通过测量得,AB=CD,BC=AD.(1)小明想起了老师的一句话:“三角形”的知识很重要很基础,以后的四边形乃至多边形的问题,常常要转化成三角形来解决.于是,他尝试着连结了AC,欣喜地发现这个四边形是平行四边形!请你循着小明的思路,说明AB∥CD,AD∥CB的理由.
解:如图,连结AC.
(2)小明又连结了BD,与AC交于点O,通过观察、分析,他得出以下结论:
①∠BAD=∠DCB,∠ABC=∠CDA;
②AO=CO,BO=DO;
③这时的图形中,有两对全等三角形;
④△AOB和△AOD的面积相等;
请你通过观察、测量、分析等方法,判断小明的这些结论中正确的个数是3个.
分析 (1)因为AB=CD,BC=AD,AC为公共边,运用SSS定理△ABC≌△CDA,利用全等三角形的性质得∠BAC=∠DCA,所以AB∥CD,同理得AD∥CB;
(2)①因为AB=CD,BC=AD,BD为公共边,运用SSS定理△ABD≌△CDB,利用全等三角形的性质得∠BAD=∠DCB,同理△ABC≌△CDA,∠ABC=∠CDA;
②因为AB∥CD,AD∥CB,利用平行线的性质,∠ABD=∠BDC,∠DAC=∠ACB,AB=CD,∠AOB=∠COD,运用AAS定理证得△AOB≌△COD,利用全等三角形的性质得,AO=CO,BO=DO;∴
③AD=CB,∠BAD=∠DCB,AB=CD,运用SAS定理,证得△ABD≌△DCB,同理证得△ABC≌CDA,所以共有四对全等三角形;
④因为BO=DO,△AOB和△AOD为等底同高的三角形,所以面积相等.
解答 证明:(1)在△ABC与△CDA中,
$\left\{\begin{array}{l}{AB=CD}\\{BC=AD}\\{AC=CA}\end{array}\right.$,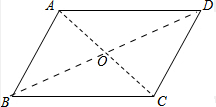
∴△ABC≌△CDA(SSS),
∴∠BAC=∠DCA,
∴AB∥CD;
在△ABD与△CDB中,
$\left\{\begin{array}{l}{AD=BC}\\{AB=CD}\\{BD=DB}\end{array}\right.$,
∴△ABD≌△CDB(SSS),
∴∠ADB=∠CBD,∴AD∥BC;
(2)①∵△ABD≌△CDB,
∴∠BAD=∠DCB;
∵△ABC≌△CDA,
∴∠ABC=∠CDA;
∴①正确;
②∵△ABD≌△CDB,
∴∠ABD=∠BDC,
在△AOB与△COD中,
$\left\{\begin{array}{l}{∠AOB=∠COD}\\{∠ABD=∠BDC}\\{AB=CD}\end{array}\right.$,
∴△AOB≌△COD(AAS),
∴AO=CO,BO=DO;
∴②正确;
③由以上结论知:
△ABC≌△CDA,△ABD≌△CDB,△AOB≌△COD,△AOD≌COD,
∴共有四对全等三角形,
∴③错误;
④∵BO=DO,△AOB和△AOD为等底同高的三角形,
∴面积相等,
∴④正确;
故答案为:3.
点评 本题主要考查了全等三角形的判定与性质,平行线的性质,选择恰当的判定条件是解决此题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )
如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{24}{25}$ | D. | $\frac{12}{25}$ |
| A. | 0 | B. | 1或9 | C. | -1或-9 | D. | 0或-1或-9 |
| 每批粒数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 发芽的粒数m | 65 | 111 | 136 | 345 | 560 | 700 |
| 发芽的频率$\frac{m}{n}$ | 0.65 | 0.74 | 0.68 | 0.69 |
(2)请估计,当n很大时,频率将接近0.70;
(3)这种玉米种子的发芽概率的估计值是但是多少?请简要说明理由.
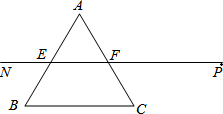 射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)
射线PN与等边△ABC的两边AB,BC分别交于点E,F,且BC∥EF,AE=BE=2cm,PF=4cm.动点Q从点P出发,沿射线PN以每秒2cm的速度向左移动,同时△ABC也沿射线PN以每秒1cm的速度向左移动,经过t秒,以点Q为圆心,$\sqrt{3}$cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值t=2或3≤t≤7或t=8.(单位:秒)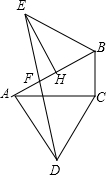 已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
已知:如图,在Rt△ABC中,∠ACB=90°,∠BAC=30°,以AC为边作等边△ACD,并作斜边AB的垂直平分线EH,且EB=AB,联结DE交AB于点F,求证:EF=DF.
 如图,⊙O的半径是4,P是⊙O内一点,且OP=3,过P点的弦AB与点O形成的△OAB的最大面积为4.
如图,⊙O的半径是4,P是⊙O内一点,且OP=3,过P点的弦AB与点O形成的△OAB的最大面积为4.